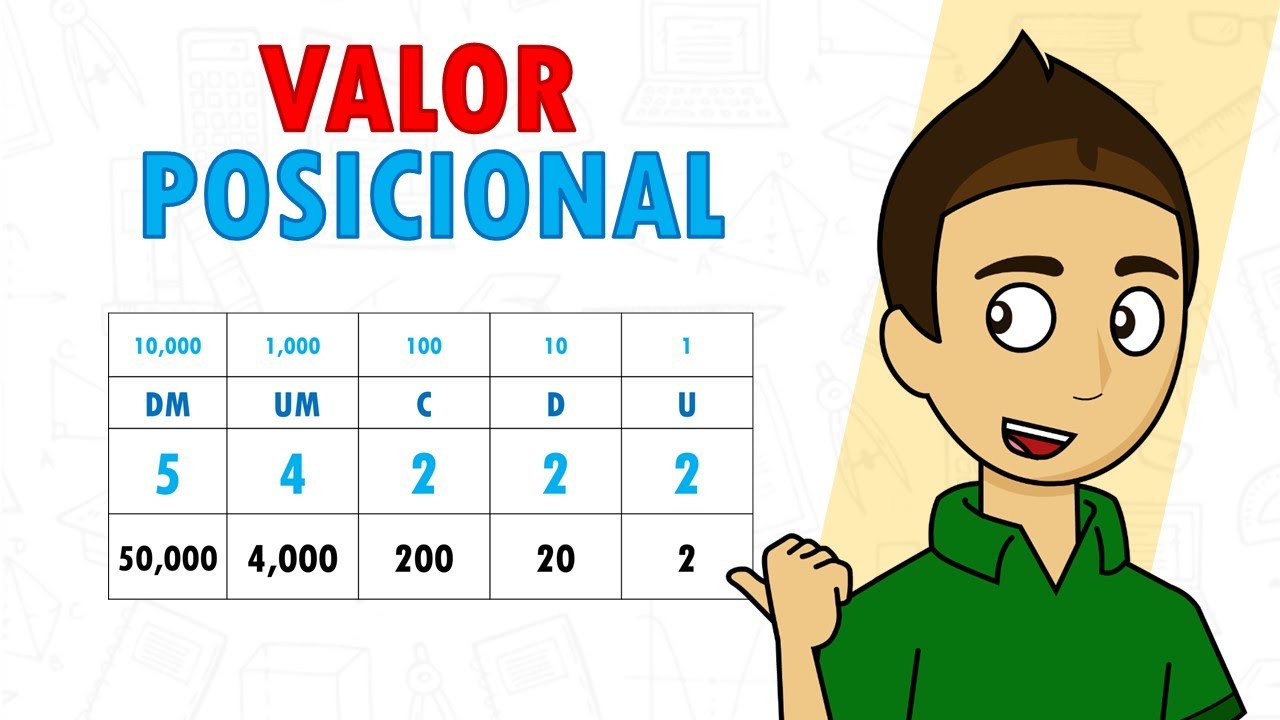
Valor Posicional de los Números: Ejemplos Claros para Entenderlo Mejor

Introducción al Valor Posicional

¿Alguna vez te has preguntado por qué el número 123 es diferente a 321? ¿O cómo es que un simple cambio de lugar de los dígitos puede alterar por completo el valor de un número? Si la respuesta es sí, estás en el lugar correcto. El concepto de valor posicional es fundamental en matemáticas y, aunque puede parecer complicado al principio, en realidad es bastante sencillo una vez que lo desglosas. Vamos a sumergirnos en este fascinante mundo de los números y descubrir juntos cómo funcionan.

El valor posicional se refiere a la importancia que tiene cada dígito dentro de un número, dependiendo de su posición. Por ejemplo, en el número 534, el 5 no tiene el mismo valor que el 3 o el 4. Aquí, el 5 representa 500, el 3 representa 30 y el 4 representa 4. ¡Interesante, verdad? Cada dígito tiene su propio «trabajo» y su propio «poder» dependiendo de dónde se encuentra. Así que, si alguna vez te has sentido confundido al ver números grandes o al realizar operaciones matemáticas, no te preocupes. Hoy desglosaremos este concepto paso a paso, usando ejemplos claros y sencillos.

¿Qué es el Valor Posicional?

El valor posicional es un sistema que usamos para entender la cantidad que representa cada dígito en un número. En nuestro sistema decimal, que es el más común, cada posición de un dígito tiene un valor basado en potencias de diez. Esto significa que el lugar donde está un número en una secuencia determina su valor real. Por ejemplo, en el número 4,562, el 4 está en la posición de los miles, el 5 en la posición de los cientos, el 6 en la posición de las decenas y el 2 en la posición de las unidades.

Imagina que cada dígito es un jugador en un equipo de fútbol. Cada jugador tiene su propio rol y posición en el campo. Si cambias a un jugador de lugar, el equipo no funcionará igual. Así es con los números. Cambiar la posición de un dígito cambia su contribución total al número. Esto es lo que hace que el sistema decimal sea tan poderoso y útil en nuestras vidas diarias.

Ejemplos Prácticos de Valor Posicional

Para entender mejor el valor posicional, vamos a analizar algunos ejemplos prácticos. Consideremos el número 2,485. Aquí, cada dígito tiene un papel importante:

– El 2 está en la posición de los miles, lo que significa que representa 2,000.
– El 4 está en la posición de los cientos, por lo que representa 400.
– El 8 está en la posición de las decenas, lo que equivale a 80.
– El 5, en la posición de las unidades, representa simplemente 5.

Si sumamos todos estos valores, obtenemos 2,000 + 400 + 80 + 5 = 2,485. Ahora, si cambiamos el 2 y el 4, obtenemos 4,285, que tiene un valor completamente diferente. ¡Es como si los números estuvieran bailando en un escenario, y cada uno tiene su propio momento para brillar!

Las Potencias de Diez y su Importancia

Ahora que hemos hablado del valor posicional, es crucial entender las potencias de diez, ya que son la base de este sistema. Cada posición en un número representa una potencia de diez. Vamos a desglosarlo:

– La posición más a la derecha es 10^0, que es 1 (unidades).
– La siguiente posición a la izquierda es 10^1, que es 10 (decenas).
– Luego, 10^2 es 100 (centenas).
– Después, 10^3 es 1,000 (miles), y así sucesivamente.

Esta estructura se repite indefinidamente. Por lo tanto, en un número como 7,654, el 7 está en la posición de los miles (10^3), el 6 en la posición de los cientos (10^2), el 5 en la posición de las decenas (10^1) y el 4 en la posición de las unidades (10^0). Así que, si alguna vez te has sentido perdido en un mar de números, recuerda que cada uno tiene su lugar y su propósito.

El Valor Posicional en la Vida Cotidiana

El valor posicional no es solo un concepto académico; está presente en nuestra vida diaria. Desde el precio de los productos en el supermercado hasta las fechas en un calendario, este sistema nos ayuda a organizar y entender la información numérica. Por ejemplo, si ves un precio de $49.99, ¿te das cuenta de que el 4 representa 40 y el 9 representa 9? Esto hace que sea mucho más fácil entender el valor total del precio.

Además, el valor posicional también es crucial en las matemáticas financieras. Al calcular intereses, impuestos o presupuestos, comprender cómo funcionan los dígitos en diferentes posiciones puede ahorrarte mucho dinero y tiempo. Así que la próxima vez que mires un número, piensa en su valor posicional y cómo se relaciona con el mundo que te rodea.

Descomponiendo Números: Una Herramienta Útil

Una excelente manera de practicar el valor posicional es descomponer números. Esto significa que tomas un número y lo divides en sus componentes individuales basados en su posición. Por ejemplo, tomemos el número 3,276. Podemos descomponerlo de la siguiente manera:

– 3,000 (3 en la posición de los miles)
– 200 (2 en la posición de los cientos)
– 70 (7 en la posición de las decenas)
– 6 (6 en la posición de las unidades)

Esto no solo te ayuda a entender mejor el número, sino que también es una excelente manera de hacer cálculos mentales más rápidos. Si necesitas sumar o restar, puedes hacerlo con cada parte por separado antes de juntar los resultados.

Ejercicios para Practicar el Valor Posicional

Ahora que has aprendido sobre el valor posicional, es hora de poner a prueba tus conocimientos. Aquí tienes algunos ejercicios que puedes hacer:

1. Descompón el número 5,432 en sus valores posicionales.
2. ¿Cuál es el valor del dígito 6 en el número 6,789?
3. Si cambias el 3 y el 5 en el número 3,256, ¿cuál será el nuevo número y su valor total?

Estos ejercicios no solo te ayudarán a practicar, sino que también te darán confianza en tus habilidades matemáticas. Así que, ¡manos a la obra!

Errores Comunes al Trabajar con el Valor Posicional

Como en cualquier habilidad, hay errores comunes que la gente tiende a cometer al trabajar con el valor posicional. Uno de ellos es olvidar la importancia de la posición. A veces, las personas piensan que los dígitos tienen el mismo valor sin importar dónde estén. Recuerda siempre que cada lugar cuenta.

Otro error es no descomponer los números cuando están realizando cálculos. A veces, se puede complicar un problema si intentas hacer todo de una vez. Descomponer los números puede simplificar mucho el proceso.

El Valor Posicional en Diferentes Sistemas Numéricos

Aunque el sistema decimal es el más común, existen otros sistemas numéricos que utilizan el valor posicional, como el binario y el hexadecimal. En el sistema binario, que es el que utilizan las computadoras, solo se utilizan dos dígitos: 0 y 1. Cada posición en un número binario representa una potencia de 2 en lugar de 10. Por ejemplo, el número binario 1011 se descompone como:

– 1 (2^3) = 8
– 0 (2^2) = 0
– 1 (2^1) = 2
– 1 (2^0) = 1

Así que, al sumar, obtendremos 8 + 0 + 2 + 1 = 11 en decimal.

Reflexiones Finales sobre el Valor Posicional

El valor posicional es un concepto esencial que nos ayuda a entender y trabajar con números de manera efectiva. Desde las matemáticas básicas hasta aplicaciones más complejas, su importancia no puede subestimarse. Al final del día, dominar el valor posicional no solo te hará más competente en matemáticas, sino que también te abrirá puertas en muchas áreas de la vida.

Así que, la próxima vez que veas un número, recuerda que hay mucho más de lo que parece a simple vista. Cada dígito tiene su propio lugar y su propio valor, ¡y ahora tú lo sabes!

Preguntas Frecuentes

• ¿Qué es el valor posicional? Es el sistema que determina el valor de un dígito en un número según su posición.
• ¿Por qué es importante el valor posicional? Es fundamental para entender cómo funcionan los números y para realizar operaciones matemáticas correctamente.
• ¿Cómo se puede practicar el valor posicional? Puedes descomponer números y hacer ejercicios de suma y resta basados en sus valores posicionales.
• ¿Existen otros sistemas de valor posicional? Sí, además del sistema decimal, hay sistemas como el binario y el hexadecimal que también utilizan el valor posicional.
• ¿Qué errores debo evitar al trabajar con el valor posicional? Olvidar la importancia de la posición y no descomponer números al realizar cálculos son errores comunes.