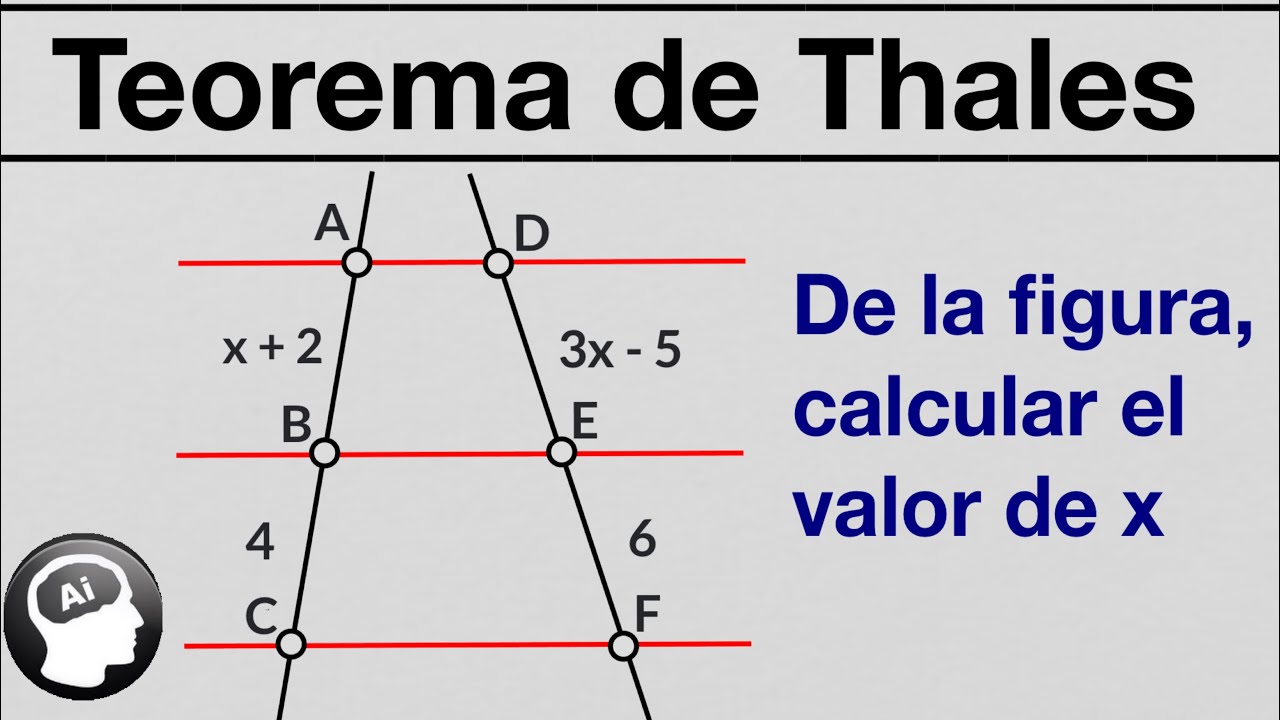
Ejercicios Resueltos del Teorema de Thales: Guía Completa para Estudiantes
Introducción al Teorema de Thales
¿Alguna vez te has preguntado cómo puedes resolver problemas de proporciones en geometría? El Teorema de Thales es una herramienta poderosa que te ayudará a entender cómo funcionan las proporciones en triángulos semejantes. En este artículo, vamos a desglosar este teorema y te proporcionaremos una serie de ejercicios resueltos que te permitirán dominar este concepto. Así que, si estás listo para convertirte en un experto en el Teorema de Thales, ¡sigue leyendo!
¿Qué es el Teorema de Thales?
Primero, hablemos de qué se trata este famoso teorema. En términos sencillos, el Teorema de Thales establece que si tienes un triángulo y trazas una línea paralela a uno de sus lados, esta línea dividirá los otros dos lados en segmentos que son proporcionales. Suena un poco técnico, ¿verdad? Pero no te preocupes, lo desglosaremos. Imagina que tienes un triángulo con vértices A, B y C, y trazas una línea paralela al lado BC que corta los lados AB y AC en los puntos D y E, respectivamente. Según el teorema, se cumple la siguiente relación de proporciones: AD/DB = AE/EC. Esto significa que los segmentos se dividen de manera proporcional, lo que es clave para resolver muchos problemas de geometría.
Aplicaciones del Teorema de Thales
El Teorema de Thales no es solo un concepto abstracto; tiene aplicaciones prácticas en la vida real. Por ejemplo, los arquitectos utilizan este teorema para escalar planos y diseños. También es útil en la navegación, donde se necesita calcular distancias y proporciones. ¡Incluso puedes encontrarlo en situaciones cotidianas, como cuando intentas medir la altura de un árbol utilizando su sombra! Así que, ¿por qué no aprovechar este conocimiento y aplicarlo a ejercicios prácticos?
Ejercicios Resueltos del Teorema de Thales
Ahora que tenemos una comprensión básica del Teorema de Thales, pasemos a algunos ejercicios resueltos. Estos ejercicios no solo te ayudarán a practicar, sino que también te permitirán ver cómo aplicar el teorema en diferentes situaciones. Te invito a que sigas cada paso, ya que esto es clave para tu aprendizaje.
Ejercicio 1: Triángulo y Línea Paralela
Supón que tienes un triángulo ABC, donde AB = 6 cm, AC = 8 cm y se traza una línea paralela a BC que corta AB en D y AC en E. Si AD = 3 cm, ¿cuánto mide DB?
Para resolver este ejercicio, aplicamos el Teorema de Thales. Sabemos que AD/DB = AE/EC. Primero, necesitamos encontrar la longitud de AE. Dado que AD + DB = AB, tenemos que 3 cm + DB = 6 cm. Por lo tanto, DB = 6 cm – 3 cm = 3 cm.
Ahora, aplicamos la proporción: 3/3 = AE/EC. Esto significa que AE = EC. Si tomamos un valor arbitrario, digamos AE = 4 cm, entonces EC también será 4 cm. Por lo tanto, la respuesta es que DB mide 3 cm.
Ejercicio 2: Escalando un Triángulo
En este caso, consideremos un triángulo DEF donde DE = 10 cm, DF = 15 cm y una línea paralela a EF corta DE en G y DF en H. Si GH = 5 cm, ¿cuánto mide EF?
Usando el Teorema de Thales, sabemos que DG/DH = GE/EF. Primero, encontramos DG. Dado que DE = 10 cm y DG = DE – GE, tenemos DG = 10 cm – 5 cm = 5 cm. Ahora, aplicamos la proporción: 5/DH = 5/EF. Esto nos lleva a EF = DH. Por lo tanto, si DH mide 7.5 cm, EF también será 7.5 cm.
Más Ejercicios para Practicar
Si has entendido los ejercicios anteriores, ¡genial! Ahora es momento de que practiques un poco más. Aquí hay algunos ejercicios adicionales que puedes intentar resolver por tu cuenta:
Ejercicio 3
En un triángulo GHI, si GH = 12 cm, GI = 16 cm y una línea paralela corta GHI en J y K, donde GJ = 4 cm. ¿Cuánto mide HK?
Ejercicio 4
Un triángulo JKL tiene JK = 20 cm, JL = 30 cm y una línea paralela corta JK en M y JL en N, donde MN = 8 cm. ¿Cuál es la longitud de LN?
Consejos para Resolver Ejercicios del Teorema de Thales
Ahora que hemos cubierto algunos ejercicios, aquí tienes algunos consejos que te ayudarán a resolver problemas del Teorema de Thales de manera más efectiva:
- Visualiza el problema: Dibuja un diagrama. Esto te ayudará a ver las relaciones entre los lados y las proporciones.
- Identifica las proporciones: Asegúrate de saber qué segmentos son proporcionales. Esto es clave para aplicar el teorema correctamente.
- Resuelve paso a paso: No te apresures. Tómate tu tiempo para resolver cada parte del problema.
- Practica, practica y practica: Cuanto más practiques, más fácil será aplicar el teorema en diferentes situaciones.
Conclusiones
El Teorema de Thales es una herramienta fundamental en la geometría que puede abrirte muchas puertas en el mundo de las matemáticas. A través de ejercicios prácticos, hemos visto cómo aplicar este teorema para resolver problemas de proporciones. Recuerda que la práctica es clave, así que no dudes en seguir practicando con diferentes problemas y ejercicios. ¿Te sientes más seguro ahora sobre el Teorema de Thales? ¡Espero que sí!
Preguntas Frecuentes
¿Qué es el Teorema de Thales en términos simples?
El Teorema de Thales establece que si una línea paralela corta los lados de un triángulo, los segmentos se dividen de manera proporcional.
¿Cómo se aplica el Teorema de Thales en la vida real?
Se utiliza en arquitectura, navegación y en diversas situaciones cotidianas donde se requiere medir proporciones y distancias.
¿Por qué es importante entender el Teorema de Thales?
Comprender este teorema te ayudará a resolver problemas de geometría y a aplicar conceptos de proporciones en situaciones reales.
¿Existen otros teoremas relacionados con el Teorema de Thales?
Sí, hay varios teoremas de semejanza de triángulos que también se relacionan con las proporciones, como el Teorema de Tales de Mileto.
¿Dónde puedo encontrar más ejercicios para practicar?
Hay muchos libros de matemáticas y recursos en línea que ofrecen ejercicios adicionales sobre el Teorema de Thales y otros conceptos de geometría.