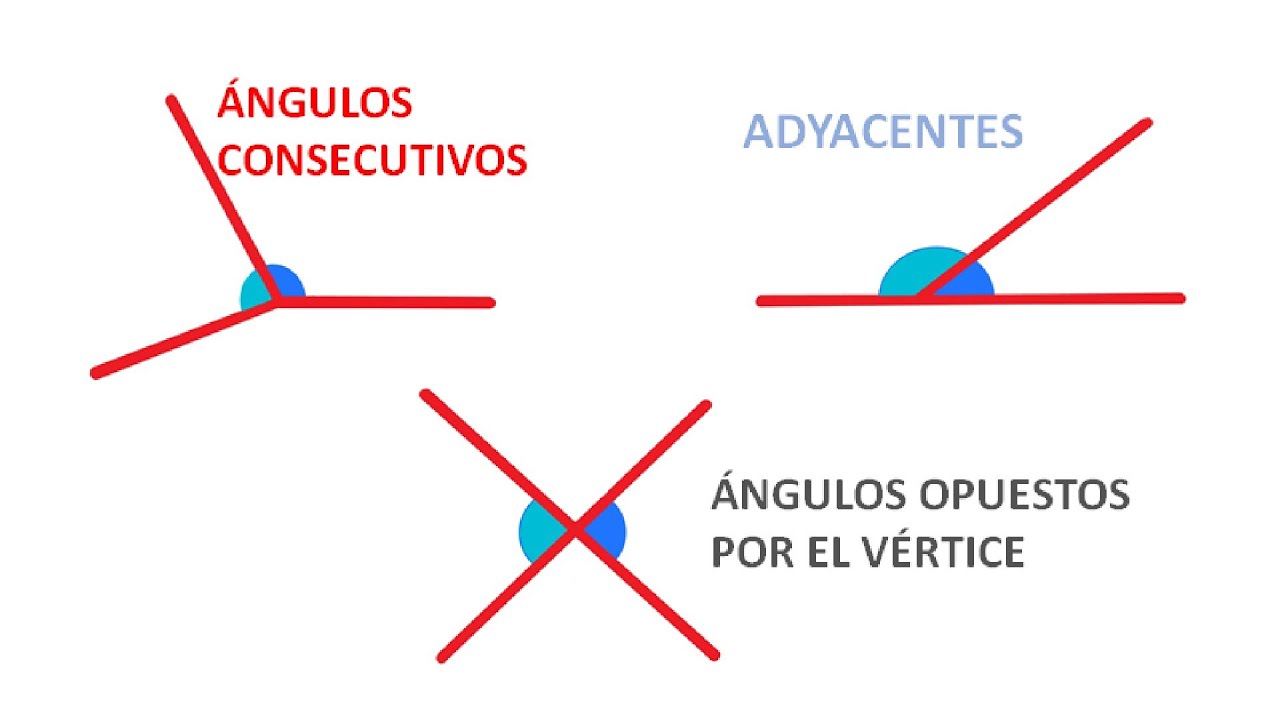
Ángulos Consecutivos, Adyacentes y Opuestos por el Vértice: Guía Completa y Ejemplos

Introducción a los Ángulos en la Geometría

¿Alguna vez te has preguntado cómo se relacionan los ángulos entre sí? Si te resulta fascinante la forma en que se conectan y se complementan, estás en el lugar correcto. Hoy vamos a explorar el intrigante mundo de los ángulos consecutivos, adyacentes y opuestos por el vértice. Este viaje no solo es útil para tus estudios de matemáticas, sino que también puede ayudarte a comprender mejor el espacio que te rodea. Así que, ¡prepárate para sumergirte en el apasionante universo de los ángulos!

¿Qué son los Ángulos Consecutivos?

Comencemos por definir qué son los ángulos consecutivos. Imagina que tienes dos ángulos que comparten un lado y un vértice, pero que no se superponen. Estos ángulos se llaman «consecutivos». Por ejemplo, si piensas en un cuadrado, los ángulos en cada esquina son consecutivos entre sí. Es como si estuvieran en una fila, uno detrás de otro, esperando su turno para brillar. Si tienes un ángulo de 30 grados y otro de 50 grados que comparten un lado, ambos son ángulos consecutivos. ¿Ves cómo se conectan?

Ejemplo de Ángulos Consecutivos

Pongamos un ejemplo práctico. Imagina que estás en una esquina de una calle. A tu izquierda, hay un ángulo de 90 grados (un ángulo recto) y a tu derecha, otro ángulo de 45 grados. Ambos ángulos comparten el vértice donde tú estás parado, y son consecutivos porque están uno al lado del otro. Si sumas estos dos ángulos, obtendrás 135 grados. Esto es importante porque en geometría, los ángulos consecutivos a menudo se utilizan para calcular ángulos más grandes o más pequeños en una figura.

¿Qué son los Ángulos Adyacentes?

Ahora hablemos de los ángulos adyacentes. Este término puede sonar similar al anterior, pero hay una diferencia clave. Los ángulos adyacentes también comparten un lado y un vértice, pero a diferencia de los ángulos consecutivos, deben estar en un plano y no pueden ser parte de un mismo ángulo. En otras palabras, los ángulos adyacentes son como dos amigos que siempre están juntos, pero cada uno tiene su propio espacio.

Ejemplo de Ángulos Adyacentes

Imagina que tienes un rombo. En cada esquina, hay ángulos adyacentes. Supongamos que en una esquina tienes un ángulo de 60 grados y en la esquina contigua, un ángulo de 120 grados. Ambos comparten un lado, pero son ángulos diferentes que no se superponen. Aquí, puedes ver que los ángulos adyacentes son fundamentales para entender la forma en que se estructuran las figuras geométricas.

¿Qué son los Ángulos Opuestos por el Vértice?

Ahora, llegamos a un concepto fascinante: los ángulos opuestos por el vértice. Imagina que estás en el centro de una intersección y observas dos pares de ángulos que se forman cuando las calles se cruzan. Los ángulos que están opuestos entre sí son los que llamamos «opuestos por el vértice». La característica más interesante de estos ángulos es que siempre son iguales. ¡Sí, has leído bien! Si uno de los ángulos mide 70 grados, el ángulo opuesto también medirá 70 grados.

Ejemplo de Ángulos Opuestos por el Vértice

Pensemos en una intersección de calles. Si un ángulo mide 30 grados, el ángulo opuesto a él, que se forma en el mismo vértice, también será de 30 grados. Esto es útil en muchas aplicaciones prácticas, desde la construcción hasta la navegación. La simetría de los ángulos opuestos por el vértice es como una danza en la que ambos se complementan perfectamente, manteniendo el equilibrio en el espacio.

Relaciones entre Ángulos Consecutivos, Adyacentes y Opuestos por el Vértice

Ahora que hemos definido cada tipo de ángulo, es hora de ver cómo se relacionan entre sí. Los ángulos consecutivos y adyacentes pueden parecer similares, pero su función es diferente en una figura geométrica. Mientras que los ángulos consecutivos se centran en la secuencia, los adyacentes se enfocan en la proximidad y la separación.

Por otro lado, los ángulos opuestos por el vértice nos ofrecen una perspectiva única. Su igualdad nos permite hacer cálculos precisos y resolver problemas complejos en geometría. En el fondo, todos estos ángulos son como piezas de un rompecabezas que, cuando se unen correctamente, crean una imagen clara y comprensible de la geometría que nos rodea.

Aplicaciones Prácticas de los Ángulos en la Vida Real

Ahora que hemos cubierto los conceptos básicos, hablemos de cómo se aplican estos ángulos en la vida real. Desde la arquitectura hasta el diseño gráfico, los ángulos juegan un papel crucial en la creación de estructuras y diseños. Por ejemplo, un arquitecto utiliza ángulos adyacentes y opuestos por el vértice al diseñar un edificio, asegurando que todo esté en equilibrio y se vea estéticamente agradable.

Ejemplos en la Arquitectura

Pensemos en una casa. La forma en que se colocan las ventanas y las puertas a menudo depende de los ángulos que se forman. Un arquitecto necesita comprender cómo los ángulos consecutivos pueden afectar la luz que entra en una habitación. Un ángulo bien diseñado puede maximizar la luz natural, haciendo que el espacio se sienta más acogedor. ¡Es como darle un abrazo cálido a tu hogar!

Cómo Calcular Ángulos Usando Relaciones de Ángulos

Calcular ángulos usando relaciones entre ángulos consecutivos, adyacentes y opuestos por el vértice puede ser muy útil. Imagina que tienes un problema de geometría en el que te piden encontrar un ángulo desconocido. Si conoces uno de los ángulos adyacentes, puedes usar la propiedad de que la suma de los ángulos adyacentes es igual a 180 grados. Esto se llama «ángulos suplementarios».

Ejemplo de Cálculo de Ángulos

Supongamos que tienes un ángulo de 110 grados y necesitas encontrar el ángulo adyacente. Dado que ambos ángulos son suplementarios, puedes restar 110 de 180. Así, 180 – 110 = 70 grados. ¡Y ahí lo tienes! Ahora conoces el valor del ángulo adyacente. Esta es solo una de las muchas formas en que puedes jugar con los ángulos y descubrir sus secretos.

Conclusión: La Importancia de Comprender los Ángulos

Comprender los ángulos consecutivos, adyacentes y opuestos por el vértice no solo es fundamental para tus estudios de matemáticas, sino que también es una habilidad valiosa que puedes aplicar en la vida diaria. Desde la construcción hasta el diseño y la resolución de problemas, los ángulos son una parte integral de cómo interactuamos con el mundo que nos rodea. Así que, la próxima vez que veas una figura geométrica, recuerda que detrás de cada ángulo hay una historia esperando ser contada.

Preguntas Frecuentes

1. ¿Los ángulos consecutivos siempre son complementarios?

No necesariamente. Los ángulos consecutivos pueden ser de cualquier medida. La clave es que comparten un lado y un vértice, pero no tienen que sumar 90 grados. Sin embargo, pueden ser complementarios si su suma es igual a 90 grados.

2. ¿Cómo se pueden usar los ángulos en la vida diaria?

Los ángulos se utilizan en diversas aplicaciones, como la construcción, la carpintería, el diseño gráfico y la navegación. Comprender cómo funcionan los ángulos puede ayudarte a tomar decisiones más informadas en estos campos.

3. ¿Qué son los ángulos suplementarios?

Los ángulos suplementarios son dos ángulos que suman 180 grados. Esta relación es útil al trabajar con ángulos adyacentes, ya que te permite calcular uno de los ángulos si conoces el otro.

4. ¿Pueden los ángulos opuestos por el vértice ser diferentes?

No, los ángulos opuestos por el vértice son siempre iguales. Esta propiedad es una de las razones por las que son tan importantes en geometría.

5. ¿Por qué es importante aprender sobre ángulos?

Aprender sobre ángulos es fundamental porque son la base de muchas áreas de las matemáticas y la ciencia. Además, entender los ángulos te ayuda a desarrollar habilidades de resolución de problemas que son útiles en la vida cotidiana.