Base y Altura de Triángulos y Paralelogramos: Guía Completa para Calcular y Entender sus Áreas
Introducción a la Geometría de Triángulos y Paralelogramos
La geometría puede parecer un tema complicado, pero si lo miras de cerca, es como un rompecabezas que se va armando poco a poco. Imagina que estás en una cocina, tratando de hacer tu platillo favorito. Para ello, necesitas ingredientes, y en el mundo de la geometría, esos ingredientes son la base y la altura de las figuras. Hoy nos centraremos en dos formas geométricas que son fundamentales: los triángulos y los paralelogramos. ¿Te has preguntado alguna vez cómo calcular su área? Bueno, ¡estás en el lugar correcto! Vamos a desglosar esto de manera sencilla y divertida.
¿Qué es un Triángulo y Cómo Calcular su Área?
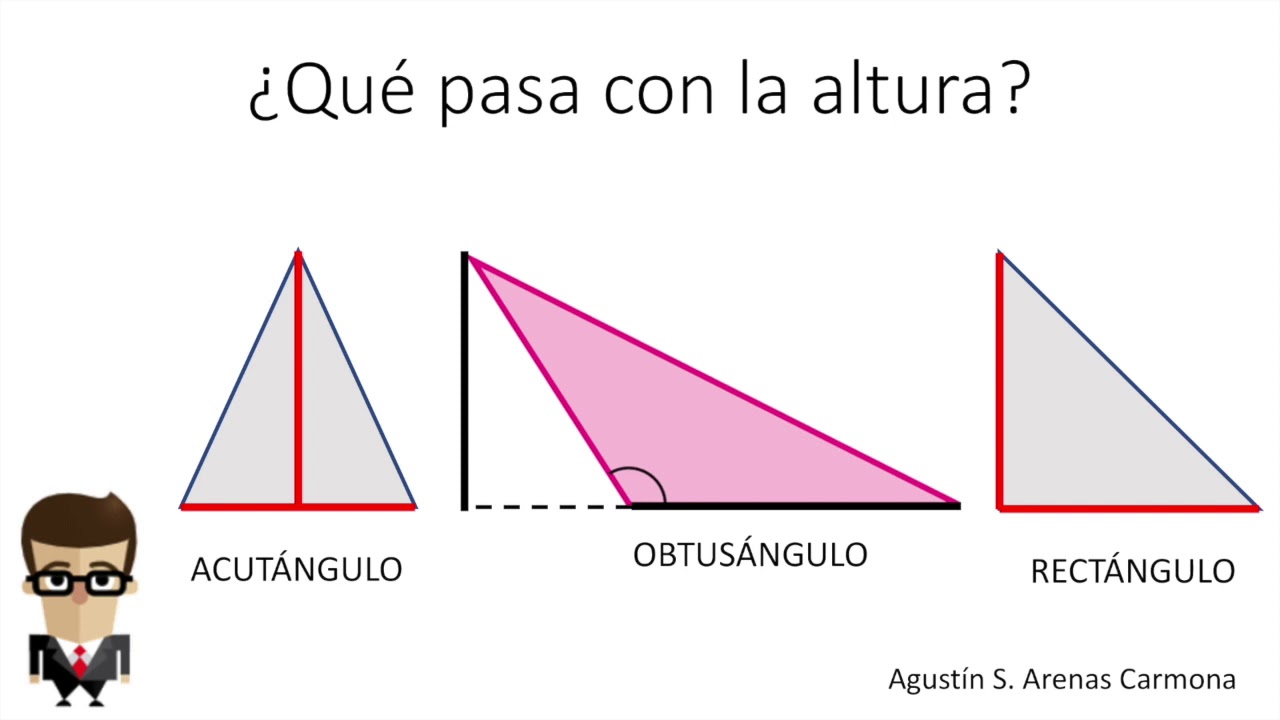
Primero, hablemos de los triángulos. Un triángulo es una figura de tres lados, y su forma puede variar desde un triángulo equilátero, donde todos los lados son iguales, hasta un triángulo escaleno, donde todos los lados son diferentes. Para calcular el área de un triángulo, necesitamos conocer dos cosas: la base y la altura. Pero, ¿qué son exactamente? La base es uno de los lados del triángulo (puede ser cualquiera de ellos), y la altura es una línea perpendicular que va desde ese lado hasta el vértice opuesto.
La fórmula para calcular el área de un triángulo es bastante sencilla: Área = (base x altura) / 2. Por ejemplo, si tienes un triángulo con una base de 8 cm y una altura de 5 cm, solo tienes que multiplicar 8 por 5, que es 40, y luego dividirlo por 2. Así que el área de tu triángulo sería 20 cm². ¿Ves lo fácil que es? Es como cortar una pizza por la mitad: tienes que conocer el tamaño de la pizza (la base) y la altura del corte para saber cuánto tienes en cada parte.
Los Tipos de Triángulos y Sus Propiedades
Ahora que hemos cubierto cómo calcular el área, hablemos un poco más sobre los diferentes tipos de triángulos. Cada tipo tiene sus propias propiedades y características que pueden influir en cómo calculas su área. Por ejemplo, en un triángulo rectángulo, donde uno de los ángulos es de 90 grados, la base y la altura son los dos lados que forman ese ángulo. Esto hace que sea súper fácil identificar cuál es la base y cuál es la altura, y puedes aplicar la fórmula del área sin complicaciones.
Triángulo Equilátero
Por otro lado, un triángulo equilátero tiene todos sus lados iguales, y para calcular su área, la cosa se complica un poco. Aquí, necesitamos una fórmula diferente: Área = (lado² * √3) / 4. Si tienes un lado de 6 cm, solo necesitas elevarlo al cuadrado, multiplicarlo por la raíz cuadrada de 3 y dividirlo por 4. Aunque puede parecer un poco más complicado, una vez que lo practiques, te sentirás como un experto en triángulos.
Paralelogramos: La Sencillez de la Simetría
Pasemos ahora a los paralelogramos. Estas figuras son un poco más sencillas en comparación con los triángulos. Un paralelogramo tiene dos pares de lados opuestos que son paralelos y de igual longitud. Lo más genial de los paralelogramos es que su área se calcula de manera muy similar a la de los triángulos, pero aquí no tenemos que preocuparnos por los ángulos. La fórmula es: Área = base x altura.
Imagina que tienes un paralelogramo con una base de 10 cm y una altura de 4 cm. Simplemente multiplicas 10 por 4, y obtienes un área de 40 cm². ¡Así de fácil! Puedes pensar en un paralelogramo como un libro abierto: la base es el ancho del libro y la altura es la distancia desde la parte inferior hasta la parte superior. La cantidad de páginas que tiene el libro (el área) depende de esos dos factores.
Comparación entre Triángulos y Paralelogramos
Ahora bien, si comparamos triángulos y paralelogramos, podemos ver que, aunque ambos tienen fórmulas sencillas para calcular su área, la forma en que lo hacemos varía. Mientras que en un triángulo necesitamos dividir por 2 debido a su naturaleza de tres lados, en un paralelogramo no es necesario. Esto es porque un paralelogramo, al tener dos pares de lados paralelos, nos da una figura más «completa».
Aplicaciones Prácticas de Áreas en la Vida Real
Calcular áreas no es solo un ejercicio académico; tiene aplicaciones prácticas en la vida real. Piensa en un jardinero que quiere plantar un nuevo jardín en forma de triángulo. Necesita saber cuánto espacio tiene para asegurarse de que tiene suficiente tierra y semillas. O imagina a un arquitecto que está diseñando una casa y necesita calcular el área de los espacios interiores. Cada centímetro cuenta. Comprender cómo calcular el área de triángulos y paralelogramos le da a la gente las herramientas necesarias para tomar decisiones informadas.
Ejemplo de Proyecto: Diseño de un Jardín
Supongamos que quieres diseñar un jardín en forma de triángulo. Si decides que la base del jardín será de 12 metros y la altura será de 5 metros, puedes aplicar la fórmula del área y descubrir que tendrás 30 m² para plantar tus flores y arbustos. ¿No es genial? Este tipo de cálculos puede hacer que tu jardín sea no solo hermoso, sino también funcional.
Preguntas Frecuentes
¿Qué sucede si no conozco la altura de un triángulo?
Si no conoces la altura, puedes usar el teorema de Pitágoras si conoces los otros lados del triángulo. Alternativamente, puedes medirla con un transportador o una regla.
¿Cómo se relacionan los triángulos y los paralelogramos en términos de área?
La relación es que un paralelogramo se puede dividir en dos triángulos. Esto significa que el área de un paralelogramo es el doble del área de uno de esos triángulos.
¿Puedo usar la misma fórmula para calcular el área de figuras irregulares?
No exactamente. Las figuras irregulares requieren métodos más complejos, como dividirlas en triángulos o paralelogramos y luego sumar sus áreas.
¿Existen otras formas de calcular áreas de triángulos?
Sí, hay varios métodos, como la fórmula de Herón, que se utiliza cuando conoces las longitudes de todos los lados. Es una herramienta útil para triángulos no rectángulos.
¿Por qué es importante aprender sobre áreas en la escuela?
Aprender sobre áreas te ayuda a desarrollar habilidades de resolución de problemas y pensamiento crítico. Además, estas habilidades son útiles en muchos campos, desde la ingeniería hasta la arquitectura y más allá.
Así que ahí lo tienes. Ya sea que estés en clase, en casa o en el jardín, entender cómo calcular áreas de triángulos y paralelogramos te dará una nueva perspectiva sobre el mundo que te rodea. ¡No dudes en poner en práctica estos conocimientos y ver cómo pueden ayudarte en tu día a día!