Ejercicios Prácticos sobre la Base y Altura de Triángulos y Paralelogramos: Mejora tu Comprensión Matemática
Descubre la Importancia de la Base y Altura en la Geometría
¡Hola, querido lector! Si alguna vez te has preguntado cómo los triángulos y paralelogramos se relacionan con la base y la altura, ¡estás en el lugar correcto! En este artículo, vamos a desglosar todo lo que necesitas saber sobre estas dos figuras geométricas, su base y altura, y cómo puedes aplicar este conocimiento a ejercicios prácticos. Pero, ¿por qué es tan importante la base y la altura? Imagina que estás construyendo una casa. Necesitas saber cuánta área ocupará el terreno, ¿verdad? Lo mismo ocurre en matemáticas. Comprender la base y la altura te ayudará a calcular áreas, resolver problemas y entender conceptos más avanzados. Así que, ¡prepárate para sumergirte en el fascinante mundo de la geometría!
¿Qué son la Base y la Altura?
Primero, vamos a definir qué son exactamente la base y la altura. La base es uno de los lados de un triángulo o paralelogramo, que se utiliza como referencia para medir la altura. Por otro lado, la altura es la distancia perpendicular desde la base hasta el vértice opuesto en un triángulo, o desde la base hasta el lado opuesto en un paralelogramo. Así que, en resumen, la base y la altura son dos componentes esenciales que nos permiten calcular el área de estas figuras. ¡Es como tener las herramientas adecuadas para un trabajo!
Fórmulas para Calcular el Área
Área de un Triángulo
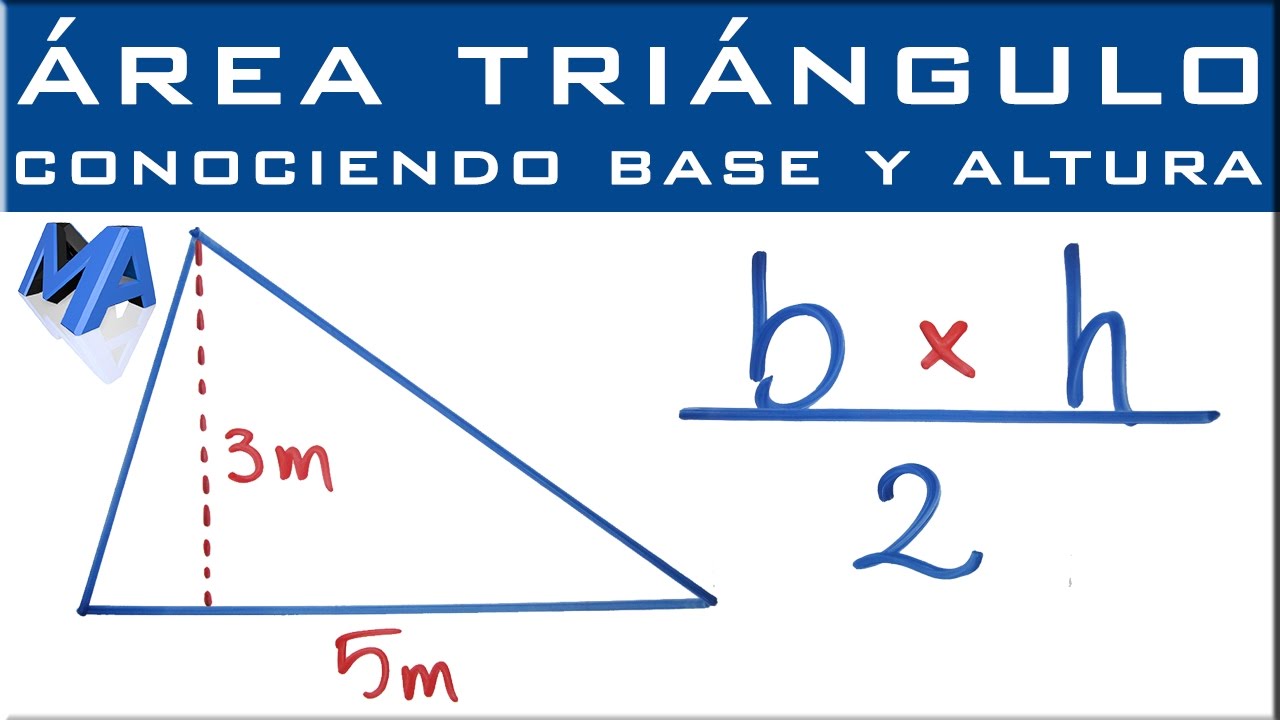
La fórmula para calcular el área de un triángulo es bastante simple y directa: Área = (Base x Altura) / 2. ¿Te suena fácil, verdad? Imagina que tienes un triángulo con una base de 8 cm y una altura de 5 cm. Si aplicamos la fórmula, el área sería (8 x 5) / 2 = 20 cm². ¡Así de sencillo! La clave aquí es recordar que siempre necesitas la altura perpendicular a la base, porque si no, los resultados pueden ser engañosos. ¡Es como intentar medir la longitud de un río siguiendo su curva, en lugar de medirlo en línea recta!
Área de un Paralelogramo
Ahora, pasemos al paralelogramo. La fórmula para calcular su área es igual de fácil: Área = Base x Altura. A diferencia del triángulo, aquí no dividimos por dos porque estamos considerando toda el área del paralelogramo. Por ejemplo, si tienes un paralelogramo con una base de 10 cm y una altura de 4 cm, el área sería 10 x 4 = 40 cm². ¿Ves cómo las matemáticas pueden ser tan satisfactorias? Es como ver cómo las piezas de un rompecabezas encajan perfectamente.
Ejercicios Prácticos para Fortalecer tu Comprensión
Ejercicio 1: Triángulo
Ahora que ya conoces las fórmulas, ¡es hora de poner en práctica lo aprendido! Imagina que tienes un triángulo cuya base mide 12 cm y su altura 7 cm. ¿Cuál es el área de este triángulo? Recuerda la fórmula: Área = (Base x Altura) / 2. Tómate tu tiempo y realiza los cálculos. Si lo hiciste bien, el área debería ser 42 cm². ¡Fantástico! ¿Ves cómo aplicar la fórmula te da resultados concretos?
Ejercicio 2: Paralelogramo
Ahora vamos a complicar un poco las cosas. Imagina que tienes un paralelogramo con una base de 15 cm y una altura de 6 cm. Usando la fórmula Área = Base x Altura, ¿cuál sería el área? Si lo calculaste correctamente, deberías obtener 90 cm². ¡Eso es! Cada ejercicio es un paso más hacia la maestría en geometría. Recuerda, la práctica hace al maestro.
Consejos para No Perderse en el Camino
Si sientes que te estás perdiendo en el proceso, aquí hay algunos consejos que pueden ayudarte. Primero, siempre dibuja un esquema de la figura. Esto te permitirá visualizar la base y la altura, lo que facilitará los cálculos. Además, asegúrate de utilizar las unidades correctas. Si tu base está en centímetros, tu altura también debe estar en centímetros para que el área esté en centímetros cuadrados. ¡Es como asegurarte de que todos los ingredientes de tu receta estén en la misma medida!
La Relevancia de la Base y la Altura en la Vida Real
Ahora bien, ¿por qué deberías preocuparte por la base y la altura más allá de los ejercicios matemáticos? La respuesta es simple: estas medidas son esenciales en muchas áreas de la vida cotidiana. Por ejemplo, si alguna vez has hecho un proyecto de jardinería, sabrás que necesitas calcular el área de un espacio para saber cuántas plantas puedes poner. O, si estás pensando en pintar una habitación, también necesitarás calcular el área de las paredes para saber cuántos litros de pintura comprar. Así que, cada vez que uses estas fórmulas, estarás aplicando matemáticas a situaciones del mundo real. ¡Eso es poderoso!
Resumiendo lo Aprendido
En resumen, hemos explorado la importancia de la base y la altura en triángulos y paralelogramos. Aprendimos las fórmulas para calcular el área de ambas figuras y realizamos ejercicios prácticos para afianzar nuestro conocimiento. Además, discutimos cómo estas medidas se aplican en situaciones cotidianas, lo que demuestra que las matemáticas no son solo un conjunto de números en una hoja, sino herramientas valiosas para la vida diaria. ¡Así que sigue practicando y no te rindas!
Preguntas Frecuentes
1. ¿Puedo usar la misma fórmula para calcular el área de un triángulo y un paralelogramo?
No, cada figura tiene su propia fórmula. Recuerda que para el triángulo divides por dos, mientras que para el paralelogramo no.
2. ¿Qué hago si no tengo la altura de la figura?
Si no tienes la altura, a veces puedes calcularla utilizando el teorema de Pitágoras, especialmente si conoces otros lados del triángulo o paralelogramo.
3. ¿Por qué es importante la altura perpendicular?
La altura perpendicular es crucial porque asegura que estés midiendo la distancia correcta desde la base hasta el vértice opuesto. Si no es perpendicular, el área calculada no será precisa.
4. ¿Hay alguna aplicación práctica de estas fórmulas en la arquitectura?
¡Absolutamente! Los arquitectos utilizan estas fórmulas para calcular áreas de espacios y determinar materiales necesarios para la construcción.
5. ¿Qué sucede si mi triángulo o paralelogramo no es un polígono regular?
Aún puedes calcular el área, pero puede que necesites dividir la figura en partes más pequeñas que sean más fáciles de manejar, como triángulos o rectángulos.
Este artículo abarca los conceptos de base y altura en triángulos y paralelogramos, proporcionando fórmulas, ejemplos y ejercicios prácticos, todo en un formato amigable y accesible. ¡Espero que te resulte útil!