Descomposición de un Número Según su Valor Posicional: Guía Completa y Ejemplos Prácticos
Introducción a la Descomposición Numérica
¿Alguna vez te has preguntado cómo descomponer un número en sus partes más simples? La descomposición de un número según su valor posicional es una habilidad fundamental que nos ayuda a entender mejor los números y su funcionamiento. En este artículo, vamos a explorar este concepto de una manera divertida y práctica. No te preocupes, no necesitas ser un genio matemático para seguirnos. Vamos a desglosar esto paso a paso, como si estuviéramos armando un rompecabezas.
La descomposición numérica no es más que la forma en que podemos expresar un número como la suma de sus partes, teniendo en cuenta el valor de cada dígito según su posición. Por ejemplo, en el número 345, el 3 no es solo un 3; representa 300. El 4, por su parte, representa 40, y el 5, simplemente, es 5. Entonces, podemos descomponer 345 en 300 + 40 + 5. ¡Fácil, verdad? Pero sigamos, porque hay mucho más que aprender sobre este tema fascinante.
¿Qué es el Valor Posicional?
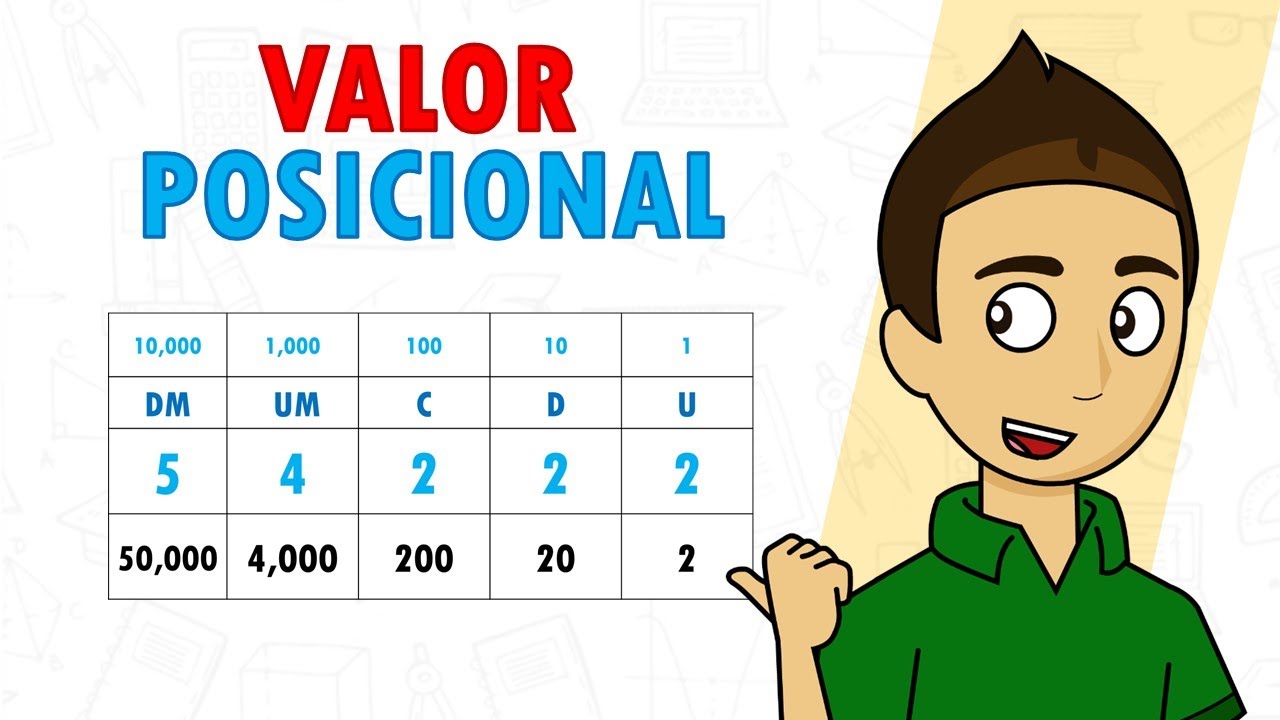
El valor posicional es un concepto clave en matemáticas. ¿Qué significa exactamente? En términos sencillos, el valor posicional se refiere a cómo el lugar donde se encuentra un dígito en un número determina su valor. En nuestro sistema decimal, que es base 10, cada posición tiene un valor que es una potencia de 10.
Por ejemplo, en el número 6789, el 6 está en la posición de miles, el 7 en la posición de centenas, el 8 en la posición de decenas y el 9 en la posición de unidades. Así que, en realidad, estamos hablando de 6000 + 700 + 80 + 9. Cada uno de esos dígitos tiene un valor específico que se multiplica por 10 elevado a la potencia correspondiente a su posición.
Ejemplos de Valor Posicional
Para aclarar un poco más, vamos a ver algunos ejemplos. Imagina el número 2045. Aquí, el 2 representa 2000 (porque está en la posición de los miles), el 0 es 0 (en la posición de las centenas), el 4 es 40 (en la posición de las decenas) y el 5 es 5 (en la posición de las unidades). Así que, de nuevo, podemos descomponerlo como 2000 + 0 + 40 + 5.
Ahora, ¿qué tal si tomamos un número un poco más complicado, como 12345? En este caso, tenemos 10000 + 2000 + 300 + 40 + 5. Cada dígito tiene su propio valor y, al descomponerlo, podemos ver cómo se suman para formar el número original.
Importancia de la Descomposición Numérica
Entender la descomposición numérica es crucial por varias razones. Primero, nos ayuda a realizar operaciones matemáticas de manera más eficiente. Cuando sumamos, restamos, multiplicamos o dividimos, conocer el valor posicional de los números nos permite descomponerlos en partes más manejables. Es como tener una caja de herramientas: cada herramienta tiene su propósito y, al combinarlas, puedes construir algo grandioso.
Además, la descomposición numérica es una base para conceptos más avanzados en matemáticas, como el álgebra. Si puedes descomponer números fácilmente, te resultará más sencillo trabajar con variables y ecuaciones. Así que, aunque pueda parecer un concepto simple, ¡en realidad es una piedra angular en tu viaje matemático!
Descomposición en la Vida Cotidiana
Quizás te estés preguntando: «¿Dónde se aplica esto en la vida real?» Bueno, la respuesta es que está en todas partes. Desde calcular el total de tu compra en el supermercado hasta gestionar tus finanzas personales, la descomposición numérica es una herramienta valiosa. Por ejemplo, si compras varios artículos y cada uno cuesta una cantidad diferente, puedes descomponer el total en partes más pequeñas para asegurarte de que no te pasas de presupuesto.
Imagina que estás en una tienda y decides comprar tres camisetas que cuestan 12, 15 y 20 dólares. En lugar de sumar directamente, puedes descomponer esos números: 10 + 2, 10 + 5 y 20. Esto no solo hace que la suma sea más fácil, sino que también te ayuda a tener un mejor control de tus gastos.
Técnicas para Practicar la Descomposición Numérica
Ahora que ya entendemos el concepto, es hora de practicar. Aquí hay algunas técnicas que puedes usar para mejorar tu habilidad en la descomposición numérica.
1. Juegos de Descomposición
Una forma divertida de practicar es a través de juegos. Puedes crear tarjetas con diferentes números y desafiarte a descomponer cada uno en su forma de suma. También hay juegos en línea y aplicaciones educativas que pueden hacer que este proceso sea más interactivo.
2. Uso de Material Manipulativo
Si eres más visual, considera usar bloques de construcción o ábacos. Estos materiales te permitirán ver físicamente cómo se descomponen los números. Por ejemplo, puedes usar bloques para representar centenas, decenas y unidades, lo que te ayudará a visualizar la descomposición de una manera más tangible.
3. Ejercicios de Escritura
Escribir es otra técnica efectiva. Toma un número y escribe su descomposición en varias formas. Esto te ayudará a interiorizar el concepto. Puedes practicar con números de diferentes longitudes y complejidades.
Errores Comunes y Cómo Evitarlos
A medida que practiques la descomposición numérica, es posible que cometas algunos errores. Aquí hay algunos de los más comunes y cómo puedes evitarlos.
1. Ignorar el Valor Posicional
A veces, la gente se olvida de que el valor de un dígito depende de su posición. Recuerda que el 5 en 5432 no es solo un 5; es 50 porque está en la posición de las decenas. Siempre verifica la posición de cada dígito antes de descomponer.
2. No Sumar Correctamente
Otro error común es no sumar correctamente las partes. Asegúrate de revisar tu trabajo. Puedes hacerlo de manera inversa, sumando las partes descompuestas para ver si obtienes el número original.
3. No Practicar Regularmente
Como cualquier habilidad, la práctica hace al maestro. Si no practicas regularmente, puedes olvidar los conceptos. Dedica unos minutos cada día a descomponer números para mantener tus habilidades afiladas.
Ejercicios Prácticos
Para poner en práctica lo que has aprendido, aquí tienes algunos ejercicios. Intenta descomponer los siguientes números:
1. 482
2. 1567
3. 3009
Tómate tu tiempo y recuerda considerar el valor posicional de cada dígito. Cuando termines, puedes comparar tus respuestas con las soluciones que te proporcionaremos al final del artículo.
Conclusión
La descomposición de un número según su valor posicional es una habilidad esencial que te acompañará a lo largo de tu vida. No solo te ayudará en matemáticas, sino que también te dará herramientas para manejar situaciones cotidianas de manera más efectiva. Así que, la próxima vez que veas un número, recuerda que detrás de él hay un mundo de posibilidades esperando a ser descompuesto.
¡Ahora es tu turno! ¿Qué número descompondrás primero? ¿Te sientes más cómodo con este concepto? La práctica te hará sentir más seguro, así que no dudes en seguir explorando y jugando con los números.
Preguntas Frecuentes
1. ¿Por qué es importante el valor posicional en matemáticas?
El valor posicional es crucial porque determina el valor de cada dígito en un número. Sin este concepto, no podríamos entender cómo funcionan los números en nuestro sistema decimal.
2. ¿Cómo puedo mejorar mis habilidades en descomposición numérica?
Puedes mejorar practicando con juegos, usando materiales manipulativos o escribiendo descomposiciones. La práctica regular es clave para dominar esta habilidad.
3. ¿La descomposición numérica se aplica a otros sistemas numéricos?
Sí, aunque el concepto de valor posicional es más evidente en el sistema decimal, también se aplica a otros sistemas numéricos, como el binario o el hexadecimal, aunque con diferentes bases.
4. ¿Hay aplicaciones que me ayuden a practicar la descomposición numérica?
Sí, hay muchas aplicaciones educativas diseñadas para ayudar a los estudiantes a practicar matemáticas, incluyendo la descomposición numérica. Busca opciones que se adapten a tu nivel y estilo de aprendizaje.
5. ¿Puedo usar la descomposición numérica para resolver problemas de álgebra?
Absolutamente. La descomposición numérica te ayuda a entender mejor cómo trabajar con variables y ecuaciones, facilitando la resolución de problemas más complejos.