Dominio y Recorrido de una Función: Guía Completa para Entender su Comportamiento
¿Qué son el dominio y el recorrido de una función?
¿Alguna vez te has preguntado cómo se comportan las funciones matemáticas? Si te has encontrado con una ecuación y no tienes idea de qué esperar de ella, no estás solo. ¡Vamos a desentrañar este misterio! En el mundo de las matemáticas, el dominio y el recorrido son conceptos fundamentales que te ayudarán a entender mejor cómo funcionan las funciones. Imagina que el dominio es como un mapa de un parque de atracciones, donde cada atracción representa un número que puedes usar como entrada. El recorrido, por otro lado, es como la lista de todas las emociones que puedes experimentar al montarte en esas atracciones. Entonces, si quieres disfrutar al máximo de la experiencia, es esencial que sepas qué esperar de cada una.
En esta guía, nos sumergiremos en estos dos conceptos esenciales, explorando sus definiciones, ejemplos y cómo puedes aplicarlos en tu vida diaria. Si alguna vez te has sentido perdido entre números y gráficos, no te preocupes. Aquí vamos a desglosarlo paso a paso, con ejemplos prácticos y explicaciones claras. Así que, ¡prepara tu mente y tu lápiz, porque estamos a punto de emprender un viaje emocionante a través del mundo de las funciones!
¿Qué es el Dominio de una Función?
El dominio de una función se refiere a todos los posibles valores de entrada (o «x») que puedes utilizar en una función sin que se produzcan problemas. Imagina que estás organizando una fiesta y necesitas saber quiénes están invitados. El dominio sería la lista completa de invitados, es decir, todos los números que puedes usar en tu función. ¿Pero cómo decidimos qué números son válidos?
Hay algunas reglas generales que debemos seguir. Por ejemplo, no podemos dividir entre cero. Si tienes una función como f(x) = 1/x, el dominio no incluiría el número cero porque no podemos dividir por cero. Otro caso común es cuando hablamos de raíces cuadradas. En la función f(x) = √x, el dominio solo incluiría números no negativos, ya que no podemos obtener una raíz cuadrada de un número negativo en el mundo de los números reales. Entonces, cuando estés tratando de encontrar el dominio de una función, asegúrate de considerar estas limitaciones.
Ejemplo Práctico del Dominio
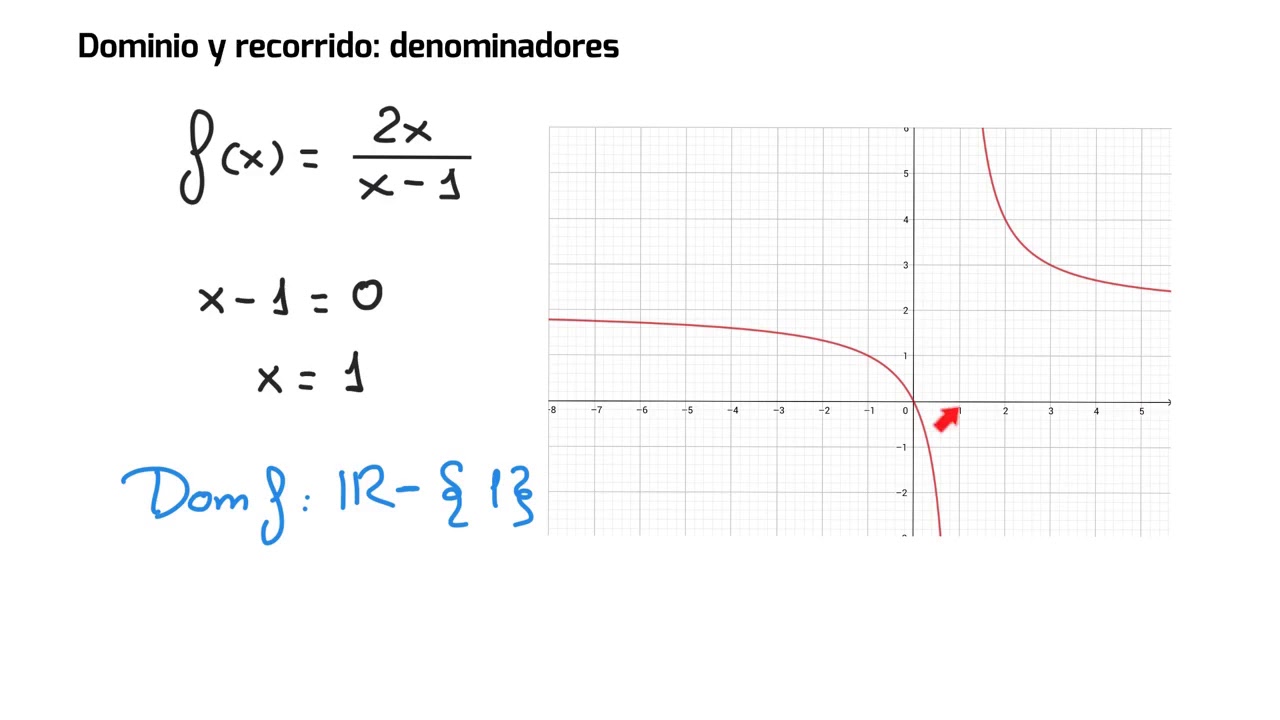
Supongamos que tienes la función f(x) = 2/(x-3). Para encontrar el dominio, primero identificamos que no podemos usar x = 3, ya que eso haría que el denominador sea cero. Por lo tanto, el dominio de esta función sería todos los números reales excepto 3. Puedes escribirlo como: D(f) = {x ∈ ℝ | x ≠ 3}. Es como tener una lista de invitados para tu fiesta, pero con un nombre que no puede estar en ella. ¿Ves cómo funciona?
¿Y el Recorrido de una Función?
Ahora que ya tenemos claro qué es el dominio, pasemos al recorrido. El recorrido se refiere a todos los posibles valores de salida (o «y») que puede tomar una función. Volviendo a nuestra analogía de la fiesta, si el dominio es la lista de invitados, el recorrido sería lo que cada invitado puede experimentar en la fiesta, como la comida, la música y las actividades. Es decir, el recorrido es el conjunto de todas las emociones o resultados que puedes obtener al usar los valores del dominio.
Para determinar el recorrido, primero necesitamos entender cómo se comporta la función. Algunas funciones son bastante predecibles, mientras que otras pueden ser un poco más complicadas. Por ejemplo, en la función f(x) = x², sabemos que el recorrido será todos los números reales no negativos, ya que el cuadrado de cualquier número siempre será cero o positivo. Así que, si piensas en ello, el recorrido de esta función sería algo así como un festín de emociones positivas.
Ejemplo Práctico del Recorrido
Considera la función f(x) = x². Ya sabemos que el dominio es todos los números reales, pero ¿qué pasa con el recorrido? Aquí, cualquier valor de x que elijas, el resultado siempre será mayor o igual a cero. Por lo tanto, el recorrido de esta función es: R(f) = {y ∈ ℝ | y ≥ 0}. Es como si solo tuvieras un buffet de postres en tu fiesta, donde todos los invitados solo pueden disfrutar de dulces y nunca de comidas saladas.
Cómo Encontrar el Dominio y el Recorrido: Pasos a Seguir
Ahora que tenemos una comprensión básica de lo que son el dominio y el recorrido, hablemos de cómo puedes encontrarlos. Esto puede sonar complicado, pero en realidad es más fácil de lo que piensas. Aquí hay algunos pasos que puedes seguir:
Paso 1: Identifica la Función
El primer paso es identificar la función que estás analizando. Puede ser una función polinómica, racional, exponencial, logarítmica, etc. Cada tipo de función tiene sus propias características que pueden afectar su dominio y recorrido.
Paso 2: Determina el Dominio
Una vez que hayas identificado la función, el siguiente paso es determinar el dominio. Revisa si hay restricciones, como divisiones por cero o raíces cuadradas de números negativos. Escribe todas las condiciones que deben cumplirse para que la función sea válida.
Paso 3: Encuentra el Recorrido
Para encontrar el recorrido, observa cómo se comporta la función. Puedes hacer esto graficando la función o analizando sus propiedades. Pregúntate: ¿cuáles son los valores que puede tomar la función? Si es una función polinómica, por ejemplo, considera los extremos y cómo se comporta en el infinito.
Paso 4: Resumen
Finalmente, resume tu hallazgo. Escribe claramente el dominio y el recorrido que has encontrado. Esto te ayudará a tener una visión clara de cómo funciona la función.
Ejemplos Adicionales para Practicar
Ahora que hemos pasado por los pasos, veamos algunos ejemplos adicionales para practicar.
Ejemplo 1: Función Lineal
Considera la función f(x) = 3x + 2.
– Dominio: No hay restricciones, por lo que el dominio es todos los números reales: D(f) = ℝ.
– Recorrido: Dado que es una función lineal, el recorrido también será todos los números reales: R(f) = ℝ.
Ejemplo 2: Función Racional
Ahora, veamos la función g(x) = (x + 1)/(x² – 4).
– Dominio: Necesitamos encontrar los valores que hacen que el denominador sea cero. x² – 4 = 0 implica que x = 2 y x = -2. Por lo tanto, el dominio es: D(g) = {x ∈ ℝ | x ≠ 2 y x ≠ -2}.
– Recorrido: El recorrido puede ser más complicado de determinar, pero generalmente implica observar el comportamiento de la función en sus límites.
La Importancia del Dominio y el Recorrido en la Vida Cotidiana
Puede que te estés preguntando, ¿por qué debería preocuparme por el dominio y el recorrido? Bueno, estos conceptos no solo son fundamentales en matemáticas; también tienen aplicaciones prácticas en la vida diaria. Por ejemplo, si estás programando un videojuego, necesitas establecer límites para las acciones de los personajes. Eso es el dominio. Y cuando consideras las diferentes reacciones de los personajes, eso es el recorrido.
En el ámbito de la economía, el dominio y el recorrido también son cruciales. Cuando modelas el comportamiento de los consumidores o las tendencias del mercado, necesitas saber qué valores son válidos y qué resultados puedes esperar. Así que, aunque puede parecer que estamos hablando de números abstractos, en realidad, estamos hablando de cómo entender el mundo que nos rodea.
Preguntas Frecuentes
¿Cuál es la diferencia entre dominio y recorrido?
El dominio se refiere a todos los posibles valores de entrada (x) que puedes usar en una función, mientras que el recorrido se refiere a todos los posibles valores de salida (y) que la función puede producir.
¿Cómo puedo encontrar el dominio de una función complicada?
Para funciones más complejas, como las que involucran raíces o fracciones, es útil identificar las restricciones que hacen que la función sea inválida. Grafica la función y observa su comportamiento para tener una mejor idea.
¿El dominio y el recorrido siempre son números reales?
No necesariamente. Dependiendo de la función, el dominio y el recorrido pueden incluir números complejos o estar restringidos a ciertos conjuntos de números, como los números enteros o los racionales.
¿Puedo tener un dominio infinito?
Sí, muchas funciones tienen un dominio que incluye todos los números reales o un intervalo infinito. Por ejemplo, las funciones polinómicas y algunas funciones exponenciales tienen dominios infinitos.
¿Es necesario conocer el dominio y el recorrido para resolver problemas matemáticos?
Sí, conocer el dominio y el recorrido te ayuda a entender mejor el comportamiento de la función y a resolver problemas de manera más efectiva. Te proporciona una base sólida para trabajar con ecuaciones y gráficas.
En resumen, el dominio y el recorrido son conceptos clave en matemáticas que te ayudarán a comprender mejor las funciones y su comportamiento. Ahora que tienes esta guía, ¡estás listo para enfrentar cualquier función que se cruce en tu camino!