Dominio y Recorrido de una Función Gráfica: Guía Completa para Entender sus Propiedades

Introducción a los Conceptos de Dominio y Recorrido

¿Alguna vez te has preguntado cómo se comporta una función gráfica? Es un tema fascinante que nos ayuda a comprender mejor cómo las matemáticas modelan el mundo que nos rodea. En este artículo, vamos a desglosar dos conceptos clave en el análisis de funciones: el dominio y el recorrido. Si alguna vez te has encontrado perdido entre números y gráficos, no te preocupes, aquí estamos para aclarar tus dudas y hacer que estos conceptos sean tan simples como un paseo por el parque.

Para empezar, hablemos del dominio. Imagina que el dominio es como la lista de invitados a una fiesta; solo las personas en esa lista pueden entrar. En términos matemáticos, el dominio de una función se refiere al conjunto de todos los valores posibles de entrada (o «x») que podemos utilizar. Por ejemplo, si tienes una función que solo acepta números positivos, entonces tu dominio estará limitado a esos números. Pero, ¿cómo determinamos cuáles son esos valores aceptables? Aquí es donde entra en juego la naturaleza de la función misma.

¿Qué es el Dominio de una Función?

El dominio es esencialmente el conjunto de todos los valores que puedes usar como entrada para tu función. Para visualizarlo, piensa en una máquina expendedora: si insertas una moneda de diez centavos, pero la máquina solo acepta monedas de un dólar, no obtendrás tu producto. De manera similar, en matemáticas, algunos valores de «x» no son válidos para ciertas funciones.

Existen varios tipos de funciones, y cada una tiene sus propias reglas sobre qué valores pueden ser parte de su dominio. Por ejemplo, en una función cuadrática como ( f(x) = x^2 ), el dominio es todo el conjunto de números reales porque puedes ingresar cualquier número y siempre obtendrás un resultado. Pero, ¿qué pasa con funciones como ( f(x) = frac{1}{x} )? Aquí, no puedes usar «0» como entrada porque dividir entre cero no tiene sentido. Entonces, el dominio de esta función sería todos los números reales excepto cero.

Cómo Encontrar el Dominio

Ahora que sabemos qué es el dominio, la pregunta es: ¿cómo lo encontramos? Hay varios métodos que puedes usar, y aquí te explicamos algunos de ellos:

1. Identificación de restricciones: Primero, debes identificar si hay alguna restricción en tu función. Si tienes raíces cuadradas, asegúrate de que lo que está dentro de la raíz sea mayor o igual a cero. Si tienes fracciones, asegúrate de que el denominador no sea cero.

2. Análisis de la función: Observa la forma de la función. Si es un polinomio, generalmente no tendrás restricciones. Pero si hay términos radicales o fraccionarios, tendrás que hacer un poco más de trabajo.

3. Pruebas numéricas: A veces, probar diferentes valores puede ayudarte a visualizar qué funciona y qué no. Si intentas diferentes números y notas que algunos no producen resultados válidos, es un indicativo de que esos números no pertenecen al dominio.

Ejemplos Prácticos del Dominio

Vamos a ver algunos ejemplos prácticos para ilustrar mejor el concepto del dominio:

– Función lineal: Para ( f(x) = 2x + 3 ), el dominio es todos los números reales. Puedes ingresar cualquier número y obtendrás un resultado válido.

– Función cuadrática: Para ( g(x) = x^2 – 4 ), el dominio también es todos los números reales. Al igual que en el caso anterior, no hay restricciones.

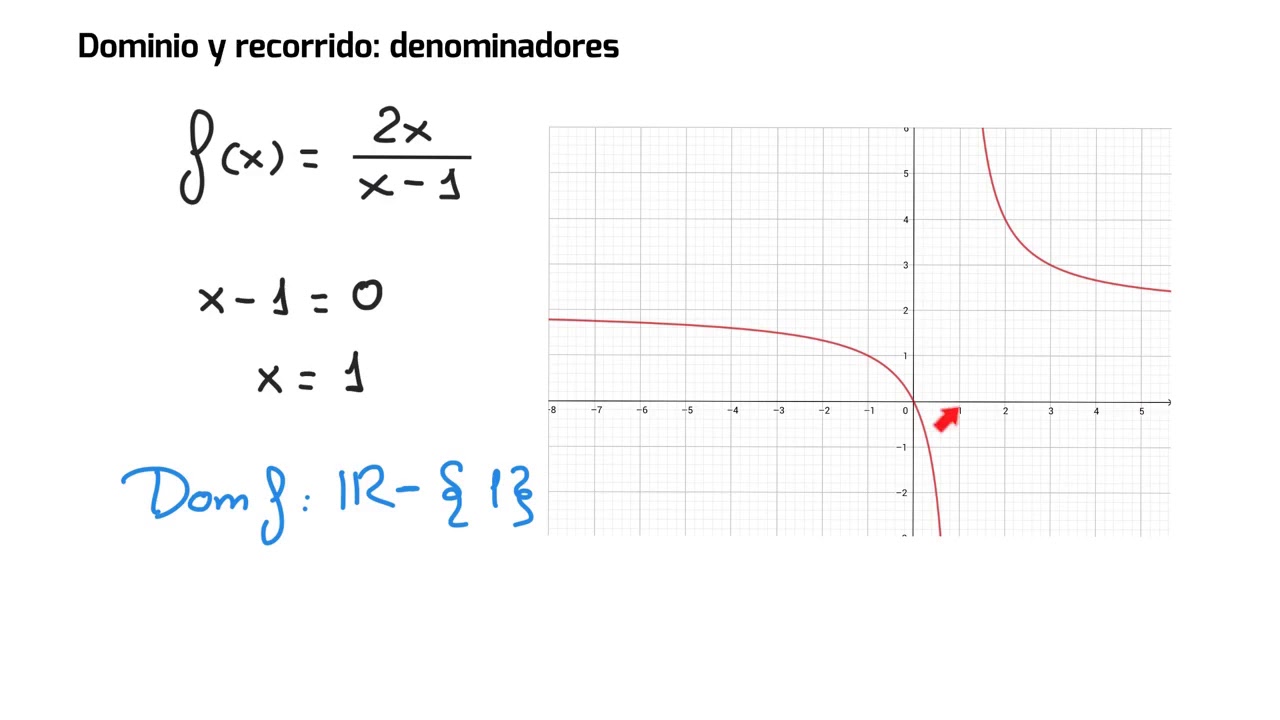
– Función racional: Para ( h(x) = frac{1}{x – 1} ), aquí hay una restricción: no puedes usar «1» como valor de entrada porque eso haría que el denominador sea cero. Por lo tanto, el dominio es todos los números reales excepto «1».

¿Qué es el Recorrido de una Función?

Ahora que hemos hablado del dominio, es hora de introducir el concepto de recorrido. Si el dominio es la lista de invitados a la fiesta, el recorrido es lo que sucede dentro de la fiesta: los resultados de las entradas que has permitido. En otras palabras, el recorrido es el conjunto de todos los posibles valores de salida (o «y») que puede producir una función.

Al igual que el dominio, el recorrido depende de la naturaleza de la función. Algunas funciones tienen un recorrido limitado, mientras que otras pueden producir una amplia gama de valores. Por ejemplo, en una función cuadrática como ( f(x) = x^2 ), el recorrido es solo valores no negativos (es decir, desde cero hasta el infinito), porque no puedes obtener un número negativo al elevar al cuadrado un número real.

Cómo Encontrar el Recorrido

Determinar el recorrido de una función puede ser un poco más complicado que encontrar el dominio. Aquí hay algunos pasos que puedes seguir:

1. Identificación de la función: Primero, identifica el tipo de función con la que estás trabajando. Las funciones lineales tienen un recorrido diferente al de las funciones cuadráticas o racionales.

2. Análisis de extremos: Observa los valores máximos y mínimos de la función. Por ejemplo, si tienes una parábola que se abre hacia arriba, su valor mínimo será el vértice, y el recorrido comenzará desde allí hacia el infinito.

3. Evaluación de límites: Para funciones más complejas, como las racionales, puedes evaluar los límites cuando «x» tiende a ciertos valores para ver qué sucede con «y».

Ejemplos Prácticos del Recorrido

Vamos a analizar algunos ejemplos del recorrido para que quede más claro:

– Función lineal: Para ( f(x) = 3x + 2 ), el recorrido es todos los números reales. Al ser una línea recta, puede tomar cualquier valor en el eje «y».

– Función cuadrática: Para ( g(x) = -x^2 + 4 ), el recorrido está limitado. Dado que la parábola se abre hacia abajo, el valor máximo es «4» (en el vértice) y el recorrido es desde menos infinito hasta «4».

– Función racional: Para ( h(x) = frac{1}{x} ), el recorrido es todos los números reales excepto «0». Esto se debe a que, a medida que «x» se acerca a cero, «y» se vuelve muy grande o muy pequeño, pero nunca toca «0».

Dominio y Recorrido en Funciones Compuestas

Cuando trabajamos con funciones compuestas, el dominio y el recorrido pueden volverse un poco más complicados. Imagina que tienes una función dentro de otra, como ( f(g(x)) ). Para determinar el dominio de esta función compuesta, debes asegurarte de que tanto el dominio de «g(x)» como el de «f(x)» se cumplan. Es decir, primero necesitas verificar que «x» esté en el dominio de «g», y luego que el resultado de «g(x)» esté en el dominio de «f».

El recorrido también puede verse afectado por la composición de funciones. Por ejemplo, si «g(x)» tiene un recorrido que se limita a ciertos valores, esto puede afectar el recorrido de la función compuesta ( f(g(x)) ).

Ejemplo de Funciones Compuestas

Supongamos que tenemos dos funciones:

– ( f(x) = x^2 ) (que tiene un dominio de todos los números reales y un recorrido de todos los números no negativos).
– ( g(x) = sqrt{x} ) (que tiene un dominio de todos los números reales no negativos y un recorrido de todos los números reales no negativos).

Si formamos la función compuesta ( h(x) = f(g(x)) = (sqrt{x})^2 ), entonces el dominio de ( h(x) ) es el mismo que el de ( g(x) ), es decir, ( x geq 0 ). El recorrido, sin embargo, será todos los números no negativos, que es el mismo que el recorrido de ( f(x) ).

Importancia del Dominio y Recorrido en la Vida Cotidiana

Ahora que hemos desglosado estos conceptos matemáticos, quizás te estés preguntando: ¿por qué son importantes? La respuesta es simple: el dominio y el recorrido no solo son fundamentales en matemáticas, sino que también tienen aplicaciones prácticas en la vida real. Desde la ingeniería hasta la economía, entender cómo funcionan las funciones puede ayudarte a resolver problemas complejos y a tomar decisiones informadas.

Imagina que eres un ingeniero que diseña un puente. Necesitas saber hasta qué punto puede soportar el peso (dominio) y qué tan alto puede llegar (recorrido). Sin esta información, podrías terminar construyendo algo que no sea seguro o funcional.

Preguntas Frecuentes

1. ¿Cómo puedo encontrar el dominio de una función cuadrática?
– Para una función cuadrática, el dominio es generalmente todos los números reales, ya que puedes ingresar cualquier número.

2. ¿El recorrido de una función siempre es igual a su dominio?
– No necesariamente. El dominio se refiere a los valores de entrada, mientras que el recorrido se refiere a los valores de salida. Pueden ser diferentes, especialmente en funciones cuadráticas y racionales.

3. ¿Cómo afecta la composición de funciones al dominio y recorrido?
– La composición de funciones puede limitar el dominio y el recorrido, ya que debes asegurarte de que los valores de salida de la función interna estén dentro del dominio de la función externa.

4. ¿Qué pasa si una función tiene un dominio restringido?
– Si una función tiene un dominio restringido, solo podrás usar esos valores específicos como entrada. Esto puede limitar los resultados que obtendrás.

5. ¿Por qué es importante entender el dominio y el recorrido?
– Comprender el dominio y el recorrido te ayuda a predecir cómo se comportará una función y es esencial en muchas aplicaciones prácticas, como la ingeniería y la economía.

Recuerda, el dominio y el recorrido son herramientas poderosas que nos ayudan a navegar por el mundo de las funciones. Al entender estos conceptos, no solo te vuelves más competente en matemáticas, sino que también abres la puerta a un mundo de posibilidades en la ciencia y la ingeniería. ¡Así que sigue explorando y no dudes en hacer preguntas!