Ejercicios Resueltos del Teorema de Pitágoras: Aprende con Ejemplos Prácticos y Soluciones Detalladas
Introducción al Teorema de Pitágoras y su Aplicación Práctica
¿Alguna vez te has preguntado cómo se relacionan los lados de un triángulo rectángulo? La respuesta está en el famoso Teorema de Pitágoras. Este teorema, que lleva el nombre del antiguo matemático griego Pitágoras, establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Pero, ¿qué significa esto realmente? Imagina que estás construyendo una casa y necesitas asegurarte de que las esquinas son perfectamente rectas. Aquí es donde entra en juego el Teorema de Pitágoras, ayudándote a calcular distancias y asegurarte de que todo esté en su lugar. En este artículo, vamos a desglosar el teorema, mostrarte ejemplos prácticos y ofrecerte ejercicios resueltos que te ayudarán a dominar este concepto matemático fundamental.
¿Qué es el Teorema de Pitágoras?
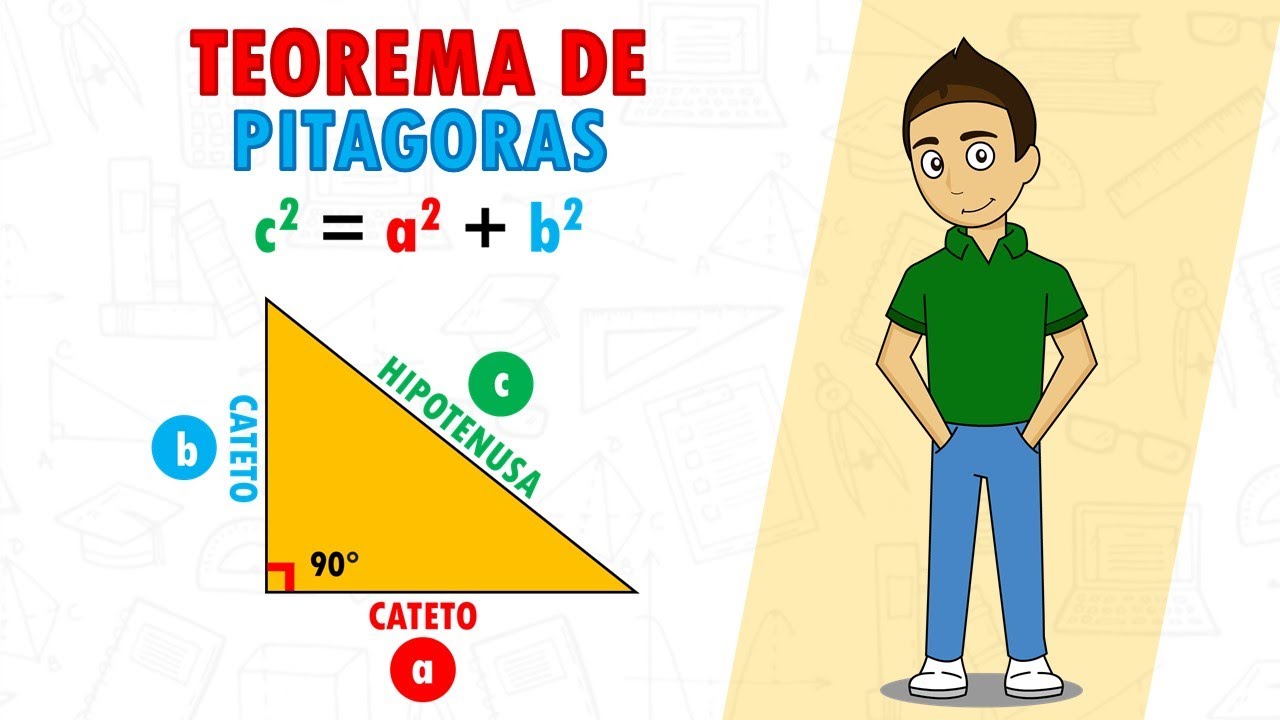
El Teorema de Pitágoras se puede expresar con la fórmula: a² + b² = c², donde a y b son las longitudes de los catetos y c es la longitud de la hipotenusa. Pero, ¿por qué es tan importante? Imagina que estás en un campo y quieres medir la distancia entre dos puntos, pero hay un río en el medio. En lugar de nadar, puedes usar el teorema para calcular la distancia más corta, formando un triángulo rectángulo. Así que, cada vez que necesites medir distancias o hacer cálculos en la vida real, el Teorema de Pitágoras será tu mejor amigo.
Ejemplo Práctico 1: Calcular la Hipotenusa
Supongamos que tienes un triángulo rectángulo donde los catetos miden 3 metros y 4 metros. ¿Cuál es la longitud de la hipotenusa? Aquí es donde aplicamos el teorema. Usamos la fórmula:
a = 3, b = 4
c² = a² + b²
c² = 3² + 4²
c² = 9 + 16
c² = 25
c = √25
c = 5
Así que, la hipotenusa mide 5 metros. ¡Fácil, verdad? Pero, ¿qué pasa si las medidas cambian? Vamos a ver otro ejemplo.
Ejemplo Práctico 2: Catetos Desconocidos
Imagina que ahora conoces la hipotenusa, que mide 10 metros, y uno de los catetos mide 6 metros. ¿Cómo encuentras el otro cateto? La fórmula sigue siendo la misma, pero ahora vamos a despejar b:
c² = a² + b²
10² = 6² + b²
100 = 36 + b²
100 – 36 = b²
64 = b²
b = √64
b = 8
Ahora sabemos que el otro cateto mide 8 metros. Con cada ejemplo, se vuelve más fácil, ¿no crees? Pero, aún hay más que explorar.
Ejemplo Práctico 3: Aplicaciones en la Vida Real
El Teorema de Pitágoras no solo es útil en matemáticas, sino que también tiene aplicaciones en diversas profesiones. Por ejemplo, los arquitectos y constructores lo utilizan para asegurarse de que las estructuras sean seguras y estéticamente agradables. Supón que estás diseñando un jardín en forma de triángulo rectángulo, y quieres saber la longitud de una diagonal que conecta dos esquinas. Si un lado mide 12 metros y el otro 9 metros, simplemente aplica el teorema:
a = 12, b = 9
c² = a² + b²
c² = 12² + 9²
c² = 144 + 81
c² = 225
c = √225
c = 15
Así que la diagonal mide 15 metros. ¡Imagina lo útil que puede ser esto al planificar espacios!
Ejercicios Resueltos: Practica con Números Reales
Ejercicio 1: Encuentra la Hipotenusa
Tienes un triángulo rectángulo donde un cateto mide 5 cm y el otro 12 cm. ¿Cuál es la longitud de la hipotenusa?
Solución:
a = 5, b = 12
c² = a² + b²
c² = 5² + 12²
c² = 25 + 144
c² = 169
c = √169
c = 13
Ejercicio 2: Cateto Desconocido
Si tienes un triángulo rectángulo con una hipotenusa de 13 cm y un cateto de 5 cm, ¿cuánto mide el otro cateto?
Solución:
c² = a² + b²
13² = 5² + b²
169 = 25 + b²
169 – 25 = b²
144 = b²
b = √144
b = 12
Más Ejercicios para Practicar
Si te sientes confiado, aquí tienes algunos ejercicios adicionales para poner a prueba tus habilidades:
- Encuentra la hipotenusa de un triángulo rectángulo con catetos de 8 cm y 15 cm.
- Si la hipotenusa mide 10 m y un cateto mide 6 m, ¿cuánto mide el otro cateto?
- Calcular la longitud de la hipotenusa de un triángulo rectángulo donde los catetos son 7 y 24.
Conclusión: Domina el Teorema de Pitágoras
El Teorema de Pitágoras es más que una simple fórmula matemática; es una herramienta poderosa que puedes usar en la vida diaria. Desde la construcción hasta la navegación, este teorema tiene aplicaciones prácticas que pueden facilitar muchas tareas. A medida que practiques más ejercicios, te sentirás más seguro al aplicar el teorema en diferentes situaciones. Recuerda, ¡la práctica hace al maestro!
Preguntas Frecuentes
¿El Teorema de Pitágoras se aplica solo a triángulos rectángulos?
Sí, este teorema es específico para triángulos rectángulos, donde uno de los ángulos mide 90 grados.
¿Cómo puedo recordar la fórmula del Teorema de Pitágoras?
Una forma fácil de recordar es pensar en la relación entre los lados: «El cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos». Puedes usar la frase «a² más b² igual a c²».
¿Puedo usar el Teorema de Pitágoras en tres dimensiones?
En tres dimensiones, el Teorema de Pitágoras se puede extender usando la fórmula d² = a² + b² + c², donde d es la distancia entre dos puntos en el espacio tridimensional.
¿Hay otros métodos para calcular distancias?
Sí, hay otros métodos, como el uso de coordenadas cartesianas y la fórmula de distancia, pero el Teorema de Pitágoras es uno de los más sencillos y visuales.
¿Puedo aplicar el Teorema de Pitágoras en situaciones cotidianas?
Absolutamente. Puedes usarlo para medir alturas, distancias en un mapa, o incluso al colgar cuadros en casa. ¡Las aplicaciones son infinitas!
Este artículo te proporciona un enfoque práctico y ameno sobre el Teorema de Pitágoras, con ejemplos y ejercicios para facilitar el aprendizaje. ¡Espero que te sea útil!