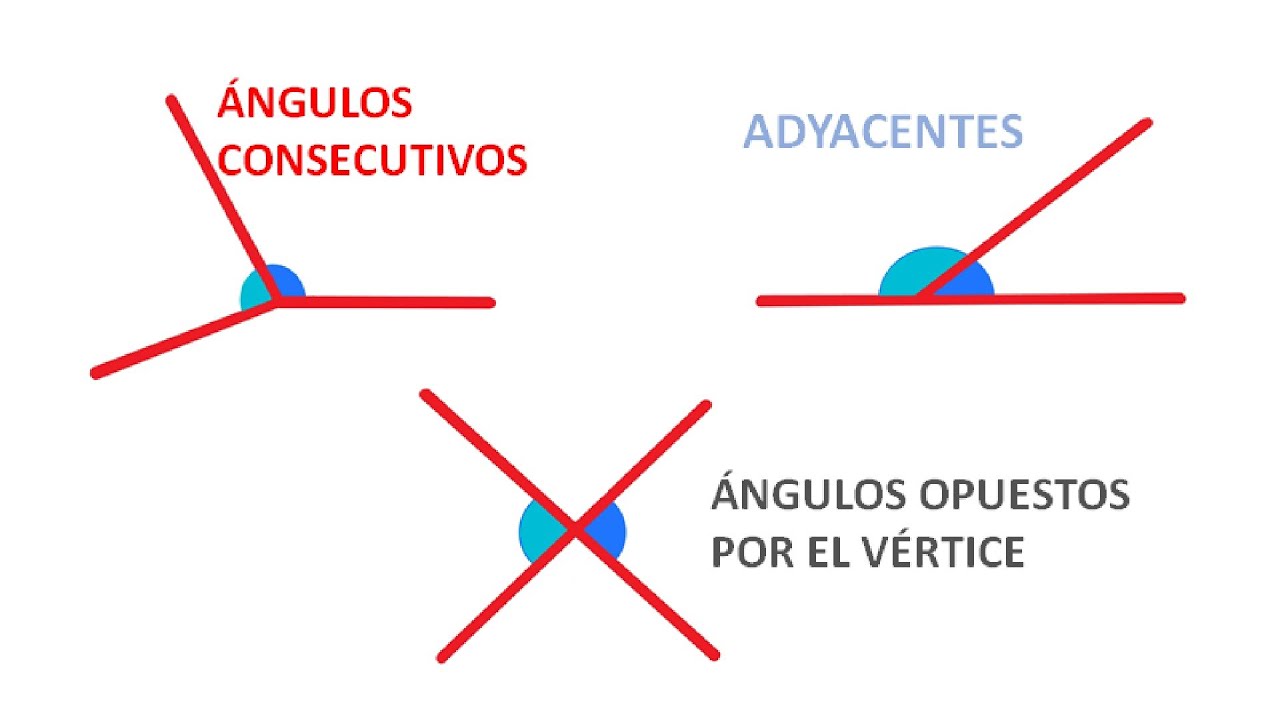
¿Por Qué Todos los Ángulos Consecutivos Son Adyacentes? Explicación y Ejemplos
Entendiendo la Relación entre Ángulos Consecutivos y Adyacentes
Cuando hablamos de geometría, hay conceptos que pueden parecer complicados a simple vista, pero que en realidad son más sencillos de lo que creemos. Uno de esos conceptos es la relación entre ángulos consecutivos y adyacentes. ¿Te has preguntado alguna vez por qué todos los ángulos consecutivos son considerados adyacentes? Bueno, aquí vamos a desglosar esta idea y explorarla de una manera que, con suerte, te hará sentir como un experto en el tema.
Definiendo Ángulos Consecutivos y Adyacentes
Primero, aclaremos qué son los ángulos consecutivos. Imagina que tienes dos ángulos que comparten un lado y un vértice, pero no se superponen. Por ejemplo, si dibujas un ángulo de 30 grados y justo al lado dibujas un ángulo de 45 grados, estos son ángulos consecutivos. Ahora, los ángulos adyacentes son aquellos que, además de ser consecutivos, también comparten un lado y un vértice, y no hay espacio entre ellos. En nuestro ejemplo, los ángulos de 30 y 45 grados se consideran adyacentes si están colocados de manera que su lado común es el mismo.
Visualizando la Relación
Para entender mejor esta relación, visualiza un reloj. Imagina que cada número en el reloj representa un ángulo. El 12 y el 1 son ángulos consecutivos porque comparten un lado (la línea que va desde el centro del reloj hasta el borde) y un vértice (el centro del reloj). Además, como están uno al lado del otro sin superponerse, son también adyacentes. Este tipo de visualización puede ayudarte a comprender cómo los ángulos se organizan en el espacio.
Propiedades de los Ángulos Adyacentes
Ahora que hemos establecido qué son los ángulos consecutivos y adyacentes, hablemos de algunas propiedades interesantes de los ángulos adyacentes. Primero, es importante destacar que la suma de los ángulos adyacentes puede ser relevante en muchas situaciones. Por ejemplo, si tienes dos ángulos adyacentes que suman 90 grados, estos se consideran complementarios. Esto se utiliza mucho en arquitectura y diseño, donde se necesita aprovechar al máximo el espacio.
Ejemplos Prácticos
Pongamos esto en práctica con un ejemplo. Imagina que estás diseñando una habitación y quieres colocar dos ventanas. Si decides que una ventana estará en un ángulo de 30 grados respecto a la pared y la otra a 45 grados, ambas ventanas son ángulos consecutivos y, si están alineadas adecuadamente, también son adyacentes. Esto te ayuda a maximizar la luz natural que entra en la habitación. Aquí, los ángulos no solo son conceptos matemáticos, sino herramientas prácticas que afectan el ambiente de tu hogar.
Aplicaciones en la Vida Cotidiana
Ahora, quizás te estés preguntando: «¿Dónde más se utilizan estos conceptos en la vida diaria?» Bueno, la respuesta es que están en todas partes. Desde la construcción hasta la decoración, los ángulos juegan un papel crucial. Por ejemplo, en carpintería, cuando se corta madera, se utilizan ángulos adyacentes para asegurar que las piezas encajen perfectamente. Un pequeño error en el ángulo puede arruinar todo el proyecto, así que la precisión es clave.
Ángulos en el Diseño Gráfico
Además, en el diseño gráfico, los ángulos adyacentes son esenciales para crear composiciones visuales atractivas. Los diseñadores a menudo utilizan ángulos para guiar la mirada del espectador y crear equilibrio. Piensa en una portada de revista; los ángulos de las imágenes y el texto se organizan de tal manera que son agradables a la vista y, al mismo tiempo, transmiten el mensaje de manera efectiva.
Un Poco de Historia
Pero, ¿de dónde proviene todo este conocimiento sobre los ángulos? La geometría, que es la rama de las matemáticas que estudia las formas y las propiedades del espacio, ha sido explorada desde la antigüedad. Los griegos, especialmente Euclides, sentaron las bases de muchos de los conceptos que hoy utilizamos. La noción de que los ángulos pueden ser clasificados y estudiados no es solo una curiosidad matemática, sino un pilar fundamental de la ciencia y la arquitectura.
Ángulos en Otras Culturas
Interesantemente, otras culturas también han hecho contribuciones significativas a la comprensión de los ángulos. Por ejemplo, en la antigua India, los matemáticos desarrollaron técnicas para medir ángulos que aún se utilizan hoy en día. Esto muestra que la curiosidad humana por comprender el espacio y las formas es un hilo común que atraviesa la historia de la humanidad.
Preguntas Frecuentes
¿Todos los ángulos consecutivos son necesariamente adyacentes?
No todos los ángulos consecutivos son adyacentes. Para que dos ángulos sean considerados adyacentes, deben compartir un lado y un vértice sin superponerse. Por ejemplo, si tienes dos ángulos que están separados por un espacio, aunque sean consecutivos, no son adyacentes.
¿Cuál es la importancia de entender los ángulos adyacentes?
Entender los ángulos adyacentes es crucial en muchas disciplinas, como la arquitectura, el diseño gráfico y la carpintería. Conocer cómo se relacionan los ángulos puede ayudarte a tomar decisiones más informadas y precisas en proyectos prácticos.
¿Pueden existir ángulos adyacentes que no sean consecutivos?
No, por definición, los ángulos adyacentes son también consecutivos. Si dos ángulos son adyacentes, necesariamente comparten un lado y un vértice, lo que implica que son consecutivos.
¿Cómo puedo practicar la identificación de ángulos adyacentes?
Una buena manera de practicar es dibujar figuras geométricas y etiquetar los ángulos. Intenta identificar cuáles son consecutivos y adyacentes. También puedes utilizar herramientas en línea o aplicaciones educativas que te ayuden a visualizar estos conceptos.
En resumen, la relación entre ángulos consecutivos y adyacentes es un concepto fascinante que tiene aplicaciones prácticas en nuestra vida diaria. Ya sea que estés diseñando una habitación, creando una obra de arte o simplemente estudiando geometría, comprender esta relación te dará una ventaja. Así que la próxima vez que te encuentres con ángulos, recuerda que son más que solo números; son herramientas que dan forma a nuestro mundo.