Triángulos según sus Lados y Ángulos: Tipos, Características y Ejemplos

Introducción a los Triángulos: Un Vistazo General

¿Alguna vez te has detenido a pensar en la belleza de un triángulo? Aunque pueda parecer una figura simple, en realidad, los triángulos son fundamentales en la geometría y en la vida cotidiana. Desde la estructura de edificios hasta el diseño de puentes, los triángulos están por todas partes. Pero, ¿sabías que hay diferentes tipos de triángulos según sus lados y ángulos? En este artículo, vamos a desglosar los tipos de triángulos, sus características y algunos ejemplos que te ayudarán a comprender mejor esta fascinante figura geométrica. Así que, ¡prepárate para adentrarte en el mundo de los triángulos!

### Tipos de Triángulos según sus Lados

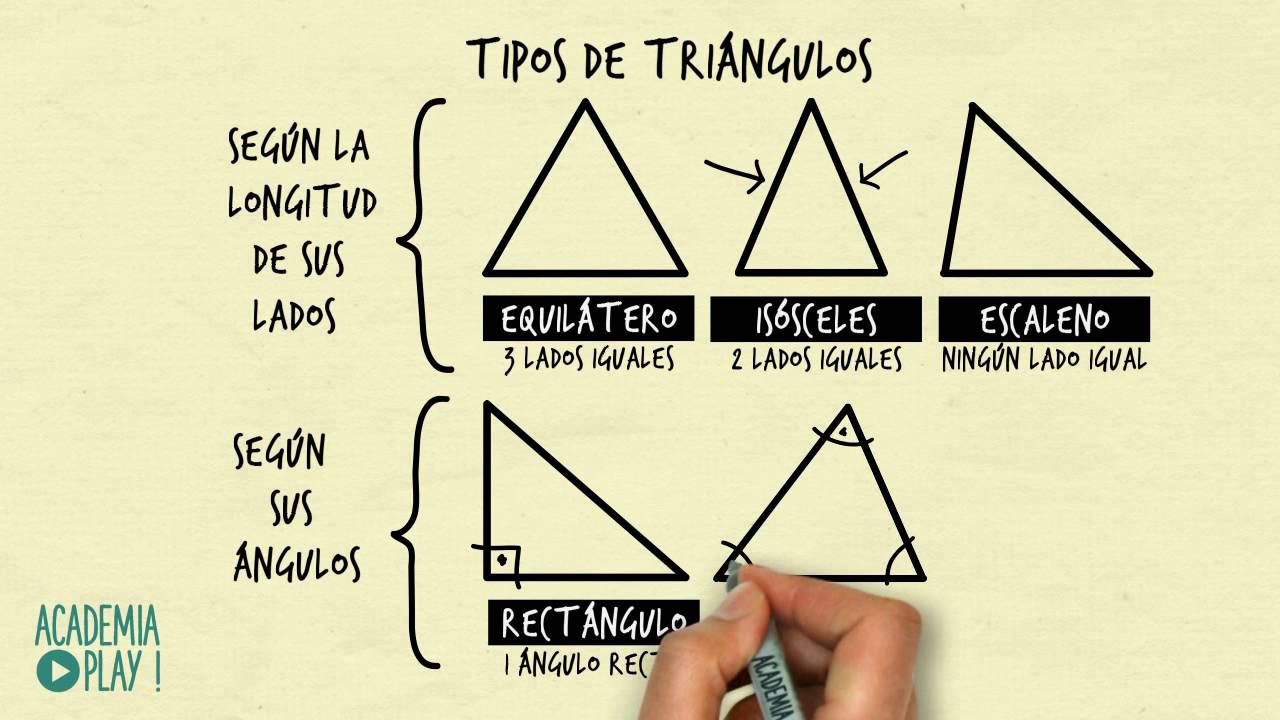
Los triángulos se pueden clasificar en tres tipos según la longitud de sus lados: equiláteros, isósceles y escaleno. Vamos a explorar cada uno de ellos para que puedas identificarlos fácilmente.

#### Triángulo Equilátero

Imagina un triángulo donde todos sus lados son iguales. ¡Eso es un triángulo equilátero! Además, no solo son iguales en longitud, sino que también sus ángulos son idénticos, cada uno mide 60 grados. Esta simetría hace que el triángulo equilátero sea visualmente atractivo y muy utilizado en diversas culturas y diseños. Por ejemplo, si alguna vez has visto una pirámide, estás mirando una estructura que se basa en triángulos equiláteros.

#### Triángulo Isósceles

Ahora, pasemos al triángulo isósceles. Este triángulo tiene al menos dos lados de la misma longitud. ¿Te suena? Sí, es como un triángulo equilátero, pero un poco menos equilibrado. Los ángulos opuestos a los lados iguales también son iguales. Un ejemplo clásico de un triángulo isósceles es el diseño de un arco, donde la simetría juega un papel crucial.

#### Triángulo Escaleno

Finalmente, tenemos el triángulo escaleno, donde todos los lados y ángulos son diferentes. Este tipo de triángulo es como un rompecabezas, cada pieza tiene su propia forma y tamaño. Aunque no tienen la simetría de los triángulos anteriores, los triángulos escalenos son igualmente interesantes. Se pueden encontrar en la naturaleza, como en ciertas formaciones rocosas.

### Tipos de Triángulos según sus Ángulos

Además de clasificarlos por sus lados, los triángulos también pueden ser clasificados según sus ángulos. Aquí es donde la cosa se pone un poco más emocionante.

#### Triángulo Acutángulo

Los triángulos acutángulos son aquellos en los que todos sus ángulos son menores de 90 grados. Imagina un triángulo que parece estar apuntando hacia arriba, con todos sus ángulos agudos. Estos triángulos son conocidos por su energía y dinamismo, y se utilizan a menudo en diseños arquitectónicos modernos.

#### Triángulo Rectángulo

El triángulo rectángulo es probablemente el más famoso de todos. Tiene un ángulo que mide exactamente 90 grados. Este tipo de triángulo es crucial en la geometría, ya que se basa en el famoso teorema de Pitágoras. Piensa en un triángulo que forma un “L” perfecto; ese es un triángulo rectángulo. Se utiliza en muchas aplicaciones, desde la construcción hasta la navegación.

#### Triángulo Obtusángulo

Por último, tenemos el triángulo obtusángulo, que tiene un ángulo mayor a 90 grados. Estos triángulos pueden parecer un poco torcidos, pero tienen su propia belleza. Un ejemplo de un triángulo obtusángulo podría ser el diseño de ciertas alas de aviones, donde la aerodinámica juega un papel importante.

### Características de los Triángulos

Ahora que hemos explorado los tipos de triángulos, hablemos de algunas características clave que todos ellos comparten.

#### La Suma de los Ángulos

Una de las propiedades más fascinantes de los triángulos es que la suma de sus ángulos siempre es 180 grados. Esto es como una regla mágica en la geometría. ¿Alguna vez te has preguntado por qué? Es un principio básico que se aplica a todos los triángulos, sin excepción. Así que la próxima vez que dibujes un triángulo, asegúrate de que los ángulos sumen 180 grados.

#### El Teorema de Pitágoras

Este es un concepto que probablemente hayas escuchado antes. El teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de los cuadrados de las longitudes de los otros dos lados. En otras palabras, si tienes un triángulo rectángulo con lados de longitud «a» y «b», y la hipotenusa de longitud «c», la fórmula es: a² + b² = c². Este teorema es fundamental en matemáticas y se utiliza en muchas áreas, desde la arquitectura hasta la navegación.

### Ejemplos Prácticos de Triángulos en la Vida Real

Los triángulos no son solo figuras abstractas; están presentes en nuestra vida diaria de muchas maneras. Aquí te dejo algunos ejemplos que te sorprenderán.

#### Arquitectura

Piensa en las estructuras que nos rodean, desde casas hasta rascacielos. Muchos de estos edificios utilizan triángulos en su diseño. Por ejemplo, los techos a menudo tienen forma triangular, lo que ayuda a distribuir el peso de manera uniforme. Esto no solo es estéticamente agradable, sino que también proporciona estabilidad y resistencia a la estructura.

#### Arte y Diseño

Los triángulos también juegan un papel crucial en el arte y el diseño gráfico. Muchos logotipos y obras de arte utilizan triángulos para crear equilibrio y simetría. Al observar un diseño, puedes notar que los triángulos guían la mirada del espectador, creando un flujo visual atractivo.

#### Navegación y Cartografía

¿Alguna vez has mirado un mapa? Muchos sistemas de navegación utilizan triángulos para calcular distancias y direcciones. Al trazar rutas en un mapa, los navegantes pueden utilizar triángulos para encontrar la mejor ruta hacia su destino. Esto se debe a que los triángulos proporcionan una manera eficiente de medir y calcular.

### Conclusión

Los triángulos son mucho más que simples figuras geométricas. Son fundamentales en nuestra vida cotidiana y están presentes en diversas disciplinas, desde la arquitectura hasta el arte y la navegación. Conocer los diferentes tipos de triángulos, sus características y aplicaciones prácticas puede ayudarte a apreciar mejor el mundo que te rodea. Así que la próxima vez que veas un triángulo, ya sea en un edificio o en un diseño gráfico, recuerda que hay mucho más detrás de esa simple figura.

### Preguntas Frecuentes

1. ¿Cómo puedo recordar los tipos de triángulos?
Una buena manera es asociar cada tipo con una imagen. Por ejemplo, un triángulo equilátero puede recordarte a una pirámide, mientras que un triángulo rectángulo puede hacerte pensar en una esquina.

2. ¿Por qué es importante el teorema de Pitágoras?
El teorema de Pitágoras es fundamental en muchas aplicaciones prácticas, como la construcción y la navegación. Te permite calcular distancias y resolver problemas en triángulos rectángulos.

3. ¿Dónde más puedo encontrar triángulos en la naturaleza?
Los triángulos pueden encontrarse en muchas formas naturales, como en las hojas de ciertas plantas, en montañas y en estructuras de cristales. La naturaleza está llena de simetría y formas geométricas.

4. ¿Pueden existir triángulos con lados negativos?
No, los lados de un triángulo siempre deben ser números positivos. En geometría, los lados negativos no tienen sentido en el contexto de la longitud.

5. ¿Cómo se relacionan los triángulos con otras figuras geométricas?
Los triángulos son la base de muchas figuras geométricas. Por ejemplo, un cuadrado puede dividirse en dos triángulos rectángulos. Además, los triángulos se utilizan para construir polígonos más complejos.

Este artículo está diseñado para ser informativo y accesible, con un estilo conversacional que mantiene al lector comprometido. Espero que te haya resultado útil e interesante.